Elementary Techniques used in the IMO (International Mathematical Olympiad) - Invariants

This post continues from both: Part 1 and Part 2

Part $3$

Applications

The first example is of a game. We will see how to apply the invariance principle.

Example 1: On a chessboard A and B play by turns to place black and white knights, respectively. Either player loses when he places a knight on a square attacked by a knight of the other colour or there are no free squares to place the knight on. If A starts, who has a winning strategy?

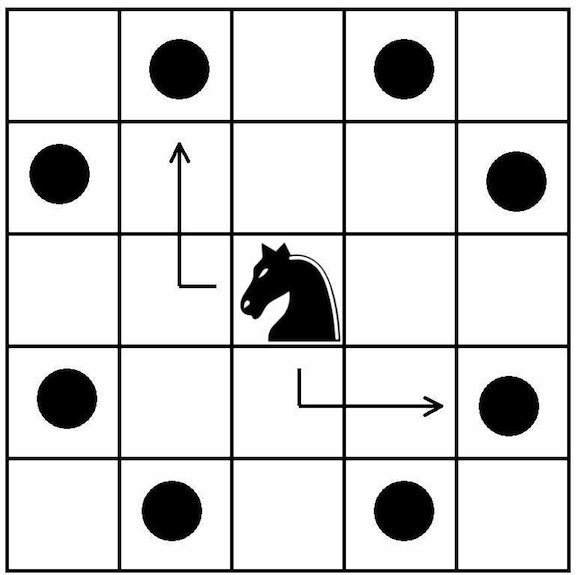
Solution: For those chess noobs like me, remark that a knight can only attack the $8$ squares shown in the figure below:

tagtext

Intuitively, if each player can place a knight such that the squares that can be attacked by both knights do not overlap, then since a chessboard has an even number of cells, Player B can win, by in what people call, mirroring the first player.

Clearly a knight on a black square can only attack a knight on a white square and vice versa. So the colours of the squares that the knight attacks is invariant. Recall that a chessboard is a $8\times 8$, so if we "fold" the board along the middle, the $2$ "flaps" would be of opposing colour. For instance, let $a_{i,j}$ be the colour of the cell in the $ith$ row and $jth$ column of the chessboard. Then we have that $a_{4,2} = a_{4,7}$.

The above observation is key for us to see that the strategy for B is to do the same thing as A but symmetric to the center of the board. Basically, notice that if A can place a knight without being attacked by B's knights, the B can always place a "symmetric" knight without being attacked by A's knight due to the colour argument. Now given the way that knights attack, A can never place a knight that attacks the square where B played. Thus A loses in the end. □

To further train the skills of the reader in solving game-like problems (because we would soon be moving to colouring and other invariance, and I would select the IMO problems for demonstration), we will attempt one more example, this problem was in my training notes, and according to our trainer, was from Bulgaria 2001.

Example 2 Alice and Bob play by turns to write ones and zeroes in a list, from left to right. The game ends when each has written 2001 numbers. When the game ends the sequence of $0 ,1$ is interpreted in base $2$. Alice wins if that number can be written as a sum of two perfect squares and if otherwise, Bob wins. Who has a winning strategy?

Solution: We want a invariant that somehow involves squares. Well, preliminarily, just plain squares would remind me of $\pmod 4$. So ultimately one should think of Fermat's Christmas Theorem. Let's see how this property translates to a winning strategy.

Now suppose the number is $1100 \ldots 0$ where there is an even number of $0$, what can you observe? (Hint: consider $\pmod 4$) Yup, exactly! Since $4m$ can be written as a sum of $2$ squares iff $m$ can, we can perfectly well ignore the zeroes at the end. And notice that $11$ in base $2$ cannot be written as a sum of $2$ squares, so B wins! Generalising this argument, at any moment A writes a $1$, B just copies $A's$ move. In this way, if we ignore the zeores, the final number would end in $11$ which is congruent to $3 \pmod 4$ which by Fermat's Christmas Theorem, cannot be written as a sum of $2$ squares, so B wins.

Now, remember that $A$ is smart. She wants to avoid losing to $B$ in this way.

Can you complete the argument? Post your completed proof in the comments.

Announcement: I am extremely sorry but since I will be going overseas and the wifi there is unsteady, I will not be posting any more of these daily instalments until Friday, Singapore time.