Elementary Techniques used in the IMO (International Mathematical Olympiad) - Invariants

I know this is much for a day, but I will be going overseas tomorrow for a long time, so I thought that It be best for me to post all the instalments and that my reader can pace himself/herself when reading through these posts.

This is the $5$th instalment, following the 4th.

At the request of Priyansh Sangule, we will do some colouring proofs today.

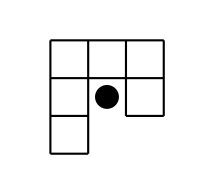
Example 4: (IMO 2004) Define a hook to be a figure made up of 6 unit squares as shown in the diagram

tagtext

or any of the tiles by applying rotations and reflections to the diagram. Determine all $m\times n$ rectangles that can covered be hooks such that:

• the rectangle is covered with hooks and no overlaps

• no part of the hook covers an area outside the rectangle.

Solution: Yet again, do not fret that we are about to attempt a considerably recent IMO problem.

We hate hooks because they are in a way disjoint. We like tiles that are nice $2 \times 3$ rectangles or things of the sort. So it is pretty motivated to consider pairs of hooks due to the hole, as marked out (with a black dot) in the following diagram:

tagtext

So necessarily if tile $X$ cover tile $Y's$ "hole", then necessarily tile $Y$ also cover the "hole" of tile $X$. We have the following $2$ pairs:

tagtext

We have our first breakthrough for this problem: $12 \mid mn$. Consider a $2 \times 6$ board. Clearly we cannot tile it with the pairs of tiles. However, we can obviously tile a $4 \times 6$ board. We might now conjecture that we must have (WLOG) that $4 \mid m$.

Let us consider the case where they are both even but $4 \nmid m,n$. So we want to find a colouring that makes use of the divisibility by $4$ condition. Well, the most direct way of incorporating it this is to add a $1$ to each cell of the board that belongs to a column or row divisible by $4$. Basically what we want to do next can then be simplified to proving that each of the pairs of hook only cover an odd number of $1$. (Do you see why this is sufficient?). Anyways, here's the board with the labelling:

tagtext

So each pair of hook clearly can only cover an odd number of $1$ by doing a simple case-bashing (I leave the reader to convince himself). So there must be an even number of tile $\rightarrow$ $4 \mid m$ (WLOG).

Now, let us summarise what we have:

• $12 \mid mn$

• $4 \mid m$

• $m,n \neq 1,2,5$ (do you see why?)

(i) So if $3 \mid n$ then we can clearly tile the whole board using the $3 \times 4$ rectangles formed from the pair of hooks.

(ii) If $12 \mid m$ and by point $3$, $m \geq 6$ then by a simple induction we can show that $m$ can be represented in the form $3a + 4b$. The motivation behind this step is that we want to be able to split up the board into smaller sections of case (i) above, because intuitively the $3 \times 4$ rectangles is more predictable than the second kind of pairing. Then all we do is that we split up the board into $a$ strips of $3 \times m$ and $b$ strips of $4 \times m$ which both can be tiled. □

Look forward to the next post, in roughly $1$ and a half weeks time, for more on colouring!