Equation of a Line

Definition

A linear equation in two variables, often written as $ y = mx + b $, describes a line in the $ xy $-plane. The line consists of all the solution pairs $ (x_0, y_0) $ that make the equation true.

For example, in the equation, $y = 2x -1$ , the line would pass through the points $(0,-1)$ and $(2, 3)$ because these ordered pairs are solutions to the equation, as is every other point on the line.

$\begin{aligned} (-1) = 2(0) -1 \\ (3) = 2(2) -1 \end{aligned}$

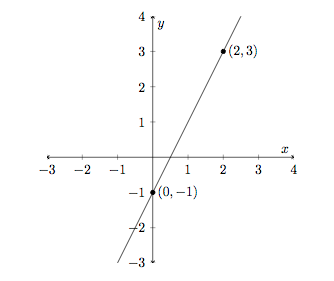A line through the points (0,-1) and (2,3)

The coefficient $m$ is the slope of the graph, and the constant $b$ is the $y$ -intercept.

The slope of a graph is the ratio between the rate of change of $y$ and the rate of change of $x$ , so for two points on a graph $p_1=(x_1,y_1)$ and $p_2=(x_2,y_2)$ , slope between them is:

$m = \frac{y_2 - y_1}{x_2-x_1}$

Technique

What is the $y$ -intercept of the line described by $2x - 3y + 9 = 0$ ?

If $2x - 3y + 9 = 0$ , then $3y = 2x + 9$ , and so $y = \frac{2}{3}x + \frac{9}{3}$ , which means the $y$ -intercept is $3$ . $_\square$

What is $a$ in the point $(-10, a)$ , if it falls on the line through the points $(2,4)$ and $(3,3)$ ?

The slope of the line is $m = \frac{(3)-(4)}{(3)-(2)}=-1$ , so $y=-x + b$ for all $x$ and $y$ on the graph. This means we can take one of the given points and substitute in its values to find $b$ .

$(3)=-(3) + b$

Therefore, $b = 6$ , and the equation of the line is $y = -x +6$ . This means the point $(-10, a)$ satisfies the equation $a = -(-10) +6$ . Thus, $a = 16$ . $_\square$

Applications and Extensions

The intersection of the line $y = 10x + 5$ with the line through the points $(1, 9)$ , $(2, 20)$ , is a point $( a , b )$ . Find the sum of $a$ and $b$ .

First, we need to find the equation of the line through $(1, 9)$ and $(2, 20)$ . Since $\frac{y_2 - y_1}{x_2-x_1} = \frac{20-9}{2-1}$ , the slope of the line must be 11. Further, since $9 = 11(1) + b$ , the $y$ -intercept is $-2$ .

Thus, our two equations are: $\begin{aligned} \mbox{Line 1: } y &= 10x_1 + 5 \\ \mbox{Line 2: } y &= 11x_2 -2 \end{aligned}$

To find the point of intersection $(a,b)$ , we solve the system of equations above by equating the two $y$ 's.

$10x + 5 = 11 x -2$

Therefore, $x = 7$ , and placing $7$ into either of the equations for $x$ gives us $(7, 75 )$ as the point of intersection. The answer, then, is $7+75 = 82$ . $_\square$

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I keep wondering at times, why is slope $m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ and not $m = \frac{x_{2} - x_{1}}{y_{2} - y_{1}}$ ? Both of them give same kind of information about the slope, one indicates the change in y per change in x and the other indicates the change in x per change in y. Is it just convention or is there some other reason to it?

Shabarish Ch - 7 years, 2 months ago

well since $m=\tan x$ , its very obvious that $m=\tan x=\frac{y_2-y_1}{x_2-x_1}$ . Stay in this pattern is also very good because in higher grades we may need to solve like "What is the equation of the line which is perpendicular with line $5x+2=0$ and pass through the point $(7,0)$ ?". Keep it $m=\tan x$ rather than $\cot x$ is more simple.

Or another way to explain is as a function $f(x)$ , $x$ is the one who "change" and $y$ is the one who "change because $x$ changed". Then as $m$ explains the different rate of change of $y$ against $x$ , then $m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$ .

Christopher Boo - 7 years, 2 months ago

Got it. Thanks.

What does line1 or line2 represent in three dimensional space?

A Former Brilliant Member - 7 years, 2 months ago

They represent two lines, since you can write them as: $0z+y=10x_1+5 \\ 0z+y=11x_2-2.$

حكيم الفيلسوف الضائع - 7 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Equation of a Line

Definition

Technique

What is the y y y-intercept of the line described by 2x−3y+9=0 2x - 3y + 9 = 0 2x−3y+9=0?

What is a a a in the point (−10,a) (-10, a) (−10,a), if it falls on the line through the points (2,4) (2,4) (2,4) and (3,3) (3,3) (3,3)?

Applications and Extensions

The intersection of the line y=10x+5 y = 10x + 5 y=10x+5 with the line through the points (1,9) (1, 9) (1,9), (2,20) (2, 20) (2,20), is a point (a,b) ( a , b ) (a,b). Find the sum of a a a and b b b.

Comments

What is the $y$ -intercept of the line described by $2x - 3y + 9 = 0$ ?

What is $a$ in the point $(-10, a)$ , if it falls on the line through the points $(2,4)$ and $(3,3)$ ?

The intersection of the line $y = 10x + 5$ with the line through the points $(1, 9)$ , $(2, 20)$ , is a point $( a , b )$ . Find the sum of $a$ and $b$ .