Exercise 2.31 cylinder and hanging mass

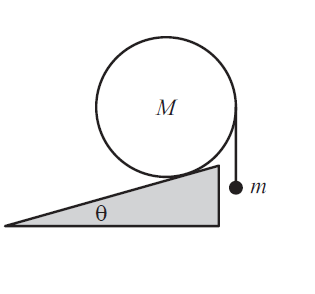
A uniform cylinder of mass $M$ sits on a fixed plane inclined at an angle $\theta$ . A string is tied to the cylinder’s rightmost point, and a mass $m$ hangs from the string, as shown in Figure above. Assume that the coefficient of friction between the cylinder and the plane is sufficiently large to prevent slipping.

What is $m$ , in terms of $M$ and $\theta$ , if the setup is static?

#Mechanics #Statics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

alt text

In the above image, I have marked out the forces on the cylinder, and also, I have removed the mass $\displaystyle m$ .

Firstly, if the system is static, then the tension in the string must be $\displaystyle mg$ , so that there is equilibrium for the mass $\displaystyle m$ .

For attaining rotational equilibrium,
Considering the torque about the contact point of the cylinder and the inclined plane,

$Mg(R\sin\theta) = T(R-R\sin\theta)$

The torque due to the Normal Reaction and the Frictional force, is zero, since those forces pass through the contact point (the point which we are considering the torque about)

$\Rightarrow Mg(R\sin\theta) = mgR(1-\sin\theta)$

$\Rightarrow M\sin\theta = m(1-\sin\theta)$

$\Rightarrow \boxed{m = \frac{M\sin\theta}{1-\sin\theta}}$

Anish Puthuraya - 7 years ago

Anish, which software do you use to draw diagrams?

Karthik Kannan - 7 years ago

I use Photoshop CS5

Anish Puthuraya - 7 years ago

@Anish Puthuraya – Oh, I don't have it. Could you recommend something else with which I can put a decent diagram?

Karthik Kannan - 7 years ago

@Karthik Kannan – Paint is not bad, if you just draw simple diagrams.

Anish Puthuraya - 7 years ago

@Anish Puthuraya – Thanks, Anish! : )

Karthik Kannan - 7 years ago

nice explanation

Hafizh Ahsan Permana - 6 years, 11 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$