Exercise 2.36 Two sticks and a wall

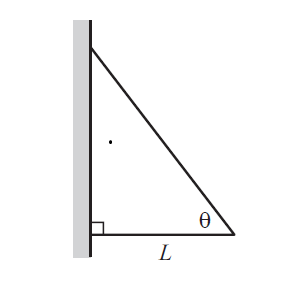
Two sticks are connected, with hinges, to each other and to a wall. The bottom stick is horizontal and has length $L$ , and the sticks make an angle of $\theta$ with each other, as shown in Figure above. If both sticks have the same mass per unit length, $\rho$ , find the horizontal and vertical components of the force that the wall exerts on the top hinge.

Also show that the magnitude goes to infinity for both $\theta$ → $0$ and $\theta$ → $\frac{\pi}{2}$

#Mechanics #Statics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

alt text

In the above figure, I have marked all the forces that are present in the system. Let the masses of the two rods be $\displaystyle m_1$ and $\displaystyle m_2$ .

Thus,
$m_1 = \rho L\sec\theta$ $m_2 = \rho L$

Considering the torque about the point A,
$h_1(L\tan\theta) = (m_1+m_2)g\frac{L}{2}$

$h_1(L\tan\theta) = \rho L (1+\sec\theta)g\frac{L}{2}$

$\boxed{h_1 = \rho\frac{1+\sec\theta}{\tan\theta}\frac{gL}{2}}$

Ill do the vertical force later..Ill post it as a comment

Anish Puthuraya - 7 years ago

Nice explanation

Mardokay Mosazghi - 7 years ago

Why are there no forces at the hinge joining the 2 sticks ??

CH Nikhil - 5 years, 10 months ago

There are forces at the hinge joining the sticks, but they are internal forces. So, they cancel each other off..

Anish Puthuraya - 5 years, 10 months ago

@Anish Puthuraya – Got it ! Thanks a lot !!

CH Nikhil - 5 years, 10 months ago

do you know any good book with exersises in rotational dynamics ;

aris nikolaidis - 6 years, 5 months ago

Try IE Irodov or Krotov

Pranjal Jain - 6 years, 4 months ago

The vertical force can be found using the pivot point B. It is -(rholg/2)(1+2sec(theta)).

Harsh Bhardwaj - 2 years, 11 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$