Fantastic Imaginary unit!

From Euler's identity : \[e^{i\theta}=\cos(\theta)+i\sin(\theta)\] For $\theta=\frac{1}{2}\pi$ \[e^{i\frac{1}{2}\pi}=i\] Let $a=e^{\frac{1}{2}\pi}$ \[\Rightarrow a^i=i \Rightarrow a^{a^{a^{a^{...}}}}=i\] Now a question which I'm unable to solve and it is very interesting one! (see tetration if you aren't understanding ${^n i}$ ) $\lim_{n \to \infty}{^n i}=?$

#Algebra

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I have plotted the graph of ${^ni}$ on the complex plain using python: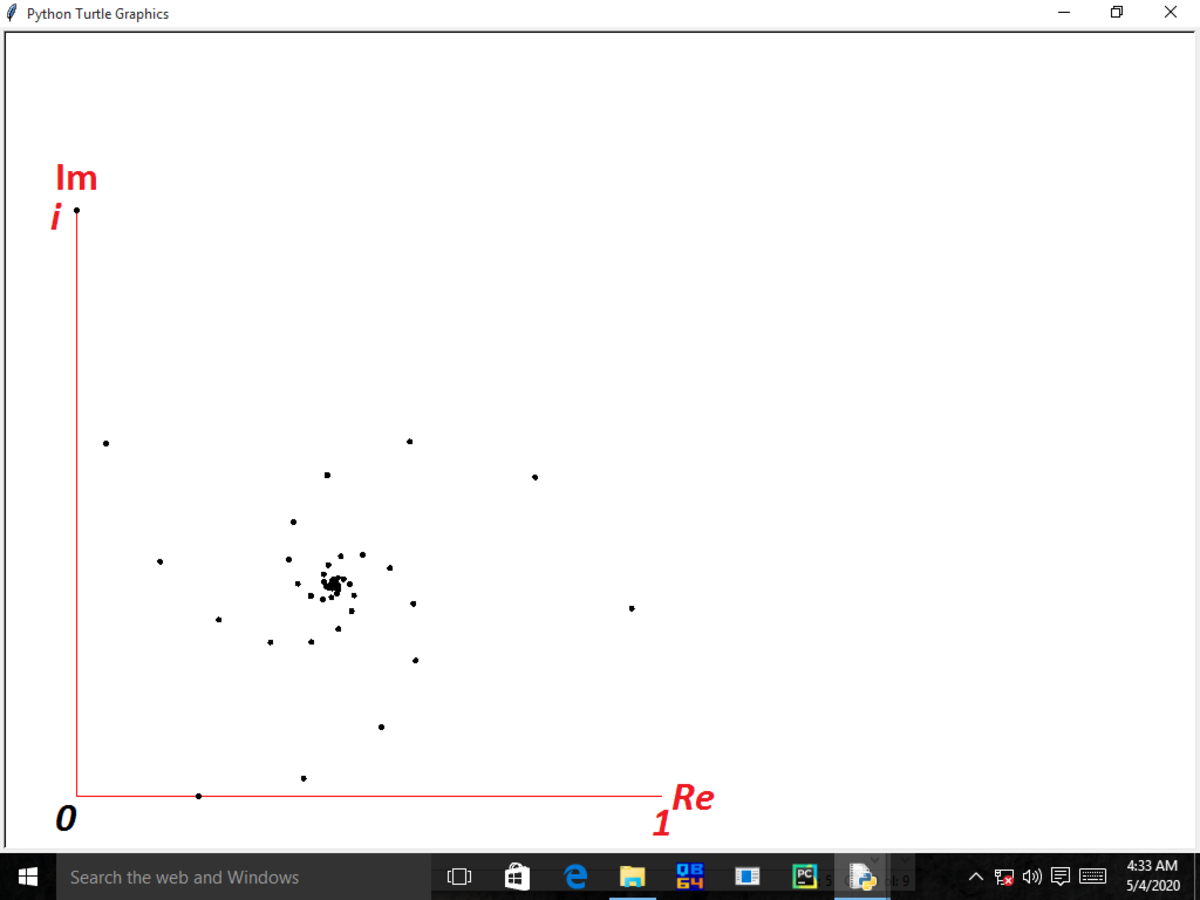 The $\lim_{n \to \infty}{^ni}$ is converging in the darker middle region.

${^{960}i}\approx 0.43828...+0.36059...i$

Zakir Husain - 1 year ago

Let the limit be $L$ . Does $i^L=L?$

Jeff Giff - 1 year ago

Yes

Justin Travers - 12 months ago

BTW, I don’t really understand $n^i,$ although I do know tetration. Could you explain it to me? Thanks :)

Jeff Giff - 1 year ago

${^ni}=i^{i^{i^{i^{.^{.^{.}}}}}}$ where there are $n$ $i's$

Sahar Bano - 1 year ago

@Sahar Bano – Well that I know... :) but $i^i$ I do not understand :D $i$ times itself $i$ times?

Jeff Giff - 1 year ago

@Jeff Giff – See how we evaluate $i^i$ :

From Euler's identity (It comes every place you talk about $i$ ): $e^{i\theta}=\cos(\theta)+i\sin(\theta)$ At $\theta = \frac{1}{2}\pi$ $e^{i\frac{1}{2}\pi}=i$ Raising both sides to $i$ $(e^{i\frac{1}{2}\pi})^i=i^i$ $i^i=(e^{i\frac{1}{2}\pi})^i=e^{\red{i}\frac{1}{2}\pi \red{i}}=e^{-\frac{1}{2}\pi}$

Zakir Husain - 1 year ago

@Zakir Husain – Oic. Thank you :)

Jeff Giff - 1 year ago

@Chew-Seong Cheong, @Justin Travers, @jordi curto, @Yajat Shamji , @Mahdi Raza, @Kumudesh Ghosh, @Alak Bhattacharya, @Vinayak Srivastava, @Aryan Sanghi, @Jeff Giff, @Marvin Kalngan

Zakir Husain - 1 year ago

Sorry but I can't be any help here since I don't know Calculus that well (I have just started the Fundamentals Course)

Kumudesh Ghosh - 12 months ago

I don't know tetration , but it seems you must calculate exponents from top to botom . Tower of "a" you equal to "i" is right if at the end of tower is and "i" . To calculate the tower you must consider where braquets are . See tetration explanation.

jordi curto - 12 months ago

Tetration of a complex number to a infinite height can be done using the Lambert W function. The formula is W(-log(z))/(-log(z)). Here log(i)=iπ/2 and the formula gives the value that Zakir Husain has calculated.

Justin Travers - 12 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$