Solve if You can ( Mechanics )

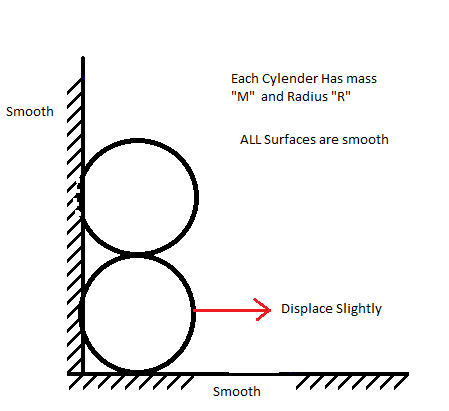
As shown in figure there is Two Identical Cylinders each of mass "M" and Radius "R". Now If Lower cylinder is displace slightly to the rightward direction then, Find The maximum Velocity of each Cylinder ?

$\bullet$ All Surfaces are smooth.

$\bullet$ Gravity is in downward direction as usual.

Please Post Solution Instead of posting answers.

Update:

Repeat this question if there is friction between the cylinders.

And Then Try question based on it Click here

#Maximum #Mechanics #Help

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Here is my method when friction is present between only cylinders. By using concept of Instantaneous centre of rotation [ ICR ]

Because This system is an equivalent Rigid Body. Since There is no relative motion between point of contact of cylinder.

Figure

The whole system is assumed to be purely rotated about "O"

Then

so velocity of any point P of this combined system in ICR ( O ) frame is given By

${ V }_{ p/o }\quad =\quad { r }_{ p/0 }\quad \times \quad { \omega }_{ 0 }$ .

${ V }_{ 1 }\quad =\quad (2R\cos { \theta } ){ \omega }_{ 0 }\\ \\ { V }_{ 2 }\quad =\quad (2R\sin { \theta } ){ \omega }_{ 0 }\\ \\ \Rightarrow \quad { \omega }_{ 0 }\quad =\quad \cfrac { \sqrt { { V }_{ 1 }^{ 2 }\quad +\quad { V }_{ 2 }^{ 2 } } }{ 2R }$ .

Now using energy conservation of system in ICR frame we get

$2gR(1-\cos { \theta } )\quad =\quad \frac { 1 }{ 2 } { I }_{ o }{ { \omega }_{ 0 } }^{ 2 }\quad \quad \quad \longrightarrow (1)\\ \\ { I }_{ o }\quad =\quad { mR }^{ 2 }\quad +{ \quad mR }^{ 2 }\quad +\quad { 4mR }^{ 2 }\cos ^{ 2 }{ \theta } \quad +{ \quad 4mR }^{ 2 }\sin ^{ 2 }{ \theta } \\ \\ { I }_{ o }\quad =\quad 6{ mR }^{ 2 }\\ \\ \\ \Rightarrow \quad { \omega }_{ 0 }\quad =\quad \sqrt { \cfrac { 2g }{ 3R } (1-\cos { \theta } ) } \quad \longrightarrow \quad (2)\\ \\ \\ { V }_{ 1 }^{ 2 }\quad =\quad \cfrac { 8gR }{ 3 } (1-\cos { \theta } )\cos ^{ 2 }{ \theta } \quad \longrightarrow \quad (3)\\ \\ \\ { V }_{ 2 }^{ 2 }\quad =\quad \cfrac { 8gR }{ 3 } (1-\cos { \theta } )\sin ^{ 2 }{ \theta } \quad \longrightarrow \quad (4)$ .

Now using maxima concept on velocity of cylinder - 1 ( Lower Cylinder )

$\cfrac { d({ V }_{ 1 }^{ 2 }) }{ d\theta } \quad =\quad 0\\ \\ \boxed { \theta \quad =\quad \cos ^{ -1 }{ \cfrac { 2 }{ 3 } } } \\ \\ Or\\ \quad \quad \\ \quad \quad \quad \quad \theta \quad =\quad 0\quad \quad \quad \times \quad (rejeccted\quad )\\ \quad \quad \quad \quad \quad \\ Or\\ \quad \quad \quad \quad \theta \quad =\quad \cfrac { \pi }{ 2 } \quad \quad \times \quad (\quad rejected\quad )$ .

So again cylinder will loose contact at the same hight as that of in 1st Part of this question ( when no friction ) I rejected other values of angle because velocity of lower cylinder never be zero. which we have discuss earlier. And Now Further Motion is independent

So we get maximum velocity of lower block

$\boxed { { V }_{ 1,max }\quad =\quad \sqrt { \cfrac { 32gR }{ 81 } } }$ .

Now velocity of 2nd cylinder can be easily calculated.

Deepanshu Gupta - 6 years, 7 months ago

I don't think that I am at that level to check your solution. But I have tried to solve the question and I got the same value of $v_{1}$ . Here is my solution.

As $r{ \omega }_{ 2 }-{ v }_{ 2 }sin\theta =r{ \omega }_{ 1 }+{ v }_{ 1 }cos\theta$

and ${ \omega }_{ 2 }={ -\omega }_{ 1 }$ .

So ${ \omega }_{ 1 }=\frac { { v }_{ 1 } }{ 2rcos\theta }$

and ${ \omega }_{ 2 }=-\frac { { v }_{ 1 } }{ 2rcos\theta }$

By energy conservation

$mg2r(1-cos\theta )=\frac { 1 }{ 2 } m{ v }_{ 1 }^{ 2 }+\frac { 1 }{ 2 } { v }_{ 2 }^{ 2 }+\frac { 1 }{ 2 } { I\omega }_{ 1 }^{ 2 }+\frac { 1 }{ 2 } { I\omega }_{ 2 }^{ 2 }$

On putting the values

$g2r(1-cos\theta )=\frac { { v }_{ 1 }^{ 2 } }{ 2{ cos }^{ 2 }\theta } +\frac { { v }_{ 1 }^{ 2 } }{ 4{ cos }^{ 2 }\theta }$

and ${ v }_{ 1 }^{ 2 }=\frac { 8gr(1-cos\theta ){ cos }^{ 2 }\theta }{ 3 }$ .

I got the same expression of $v_{1}$ .

Deepanshu and Mvs ,what you guys think about my method. Is this correct?

satvik pandey - 6 years, 7 months ago

your answer as far as i can comprehend seems absolutely correct

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – Please clear my last confusion. I have found that ${ \alpha }_{ 1 }=-{ \alpha }_{ 2 }$ but how do we show ${ \omega }_{ 1 }=-{ \omega }_{ 2 }$

I have tried

as ${ \alpha }_{ 1 }=-{ \alpha }_{ 2 }$

so $\frac { d{ \omega }_{ 1 } }{ dt } =-\frac { d{ \omega }_{ 2 } }{ dt }$

or $\int { d{ \omega }_{ 1 } } =-\int { d{ \omega }_{ 2 } }$

or ${ \omega }_{ 1 }=-{ \omega }_{ 2 }+C$

At $t=0$ ${ \omega }_{ 1 }={ \omega }_{ 2 }=0$ So $C=0$

So ${ \omega }_{ 1 }=-{ \omega }_{ 2 }$

Is that how you proved ${ \omega }_{ 1 }=-{ \omega }_{ 2 }$ ?

@Mvs Saketh and @DEEPANSHU GUPTA please reply.

satvik pandey - 6 years, 7 months ago

@Satvik Pandey – I think we are wrong with the rotational part,, please observe carefully,, i have been pondering over this contradiction for long and hence i have not posted any solution when rotation comes into play,,

heres what we have

w1=w2

also that $r{ w }_{ 1 }-{ v }_{ 2 }sin\theta \quad =\quad r{ w }_{ 1 }+{ v }_{ 1 }cos\theta$

as w1=w2 so rw1=rw2, thus cancelling like terms

$-{ v }_{ 2 }sin\theta \quad =\quad { +v }_{ 1 }cos\theta$ ...(1)

now already through translatory constraint

we have ${ v }_{ 2 }cos\theta \quad =\quad { +v }_{ 1 }sin\theta$ ...(2)

dividing one and 2 , we get

$tan\theta \quad =\quad -cot\theta$ which is not true for all angles,, clearly we are wrong,, i do not know where,, i do now know how,, but i would say we are wrong,, this is giving contradictory results,, either this means that such a situation is not possible or that we are missing something

@DEEPANSHU GUPTA @satvik pandey

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – The equation is $r{ \omega }_{ 2 }-{ v }_{ 2 }sin\theta =r{ \omega }_{ 1 }+{ v }_{ 1 }sin\theta$ (I think you typed it wrong there. You wrote w1 instead of w2) and also $\omega_{1}=- \omega_{2}$ (you missed that minus sign). If I am not wrong I think you are getting this result due to wrong signs.

satvik pandey - 6 years, 7 months ago

@Satvik Pandey – no w1=w2 is okay i am comparing magnitudes,, but yes wrong signs actually i do not know yet whether rw2 greater or v2 sin(x) so my contradiction arises because i am assuming rw2 is greater and the contradiction shows that such a case is never possible

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – Saketh you have done mistake in calculation of Constrained ..!! Check again !!

And Satvik your solution is Partially incorrect. !!

See carefully What is I'am Trying to Saying ...!!

Fig-1 Fig-1

Now Since Cylinder are Rolling without slipping so There is no relative motion along common Tangent.

${ \omega }_{ 2 }R\quad -\quad { V }_{ 2 }\sin { \theta } \quad =\quad { V }_{ 1 }\cos { \theta } -\quad \quad { \omega }_{ 1 }R\quad \quad ...........\quad (1)$ .

Now Since Rod is Rigid So there is no relative motion between cylinders along Common Normal .

${ V }_{ 2 }\cos { \theta } \quad =\quad { V }_{ 1 }\sin { \theta } \quad \quad .................(2)$ .

Now By writing Torque equation we get :

${ \alpha }_{ 1 }\quad =\quad \frac { fR }{ I } \quad \quad (\quad Anti\quad clock\quad wise\quad )\\ \\ { \alpha }_{ 2 }\quad =\quad \frac { fR }{ I } \quad (\quad Anti\quad Clock\quad wise\quad )\\ \\ { \alpha }_{ 1 }\quad =\quad { \alpha }_{ 2 }$ .

Now after integrating it and put limits we get

${ \omega }_{ 1 }\quad =\quad { \omega }_{ 2 }\quad ........................\quad (3)$ .

So @satvik pandey Your Method is incorrect . But Your Final expression for ${ V }_{ 1 }$ . as a function of theta is correct .

Because in energy equation :

$\boxed { \\ { { (-\omega }_{ 1 }) }^{ 2 }{ { \quad =\quad (\omega }_{ 1 }) }^{ 2 } }$ .

And If You want more Rigorous Proof of the fact that

$\boxed { { \omega }_{ 1 }\quad =\quad { \omega }_{ 2 } }$ .

Then I would say that In My solution I used ICR .. and calculate ${ \omega }_{ ICR }\quad =\quad { \omega }_{ 0 }$ .

Note That this system ( both cylinder ) is considers as rigid Body ( not discrete because there is no relative motion between them ) So according to fundamental rule of Rotational Dynamics that all Rotational Parameters Like as $\\ { \alpha }\quad ,{ \quad \omega }\quad etc.$ . would remain same about all Point's on Rigid body system.

So In Fact

$\boxed { { \omega }_{ 1 }\quad =\quad { \omega }_{ 2 }\quad ={ \quad \omega }_{ ICR }\quad =\quad { \omega }_{ 0 }\quad =\quad ...........(Any\quad Point)\quad \quad }$ .

Hope This might be Helps You !!

Deepanshu Gupta - 6 years, 7 months ago

@Deepanshu Gupta – I tried a non energy method and am getting a completely different answer. Can you please help me out by checking my solution?

Here a{1} : Acceleration of upper cylinder in downward dir. And a{2} : Acceleration of lower cylinder in horizontal dir. N , f : Normal reaction and friction(As in your diagram above) at point of contact. Theta: Angle made by line joining centres with the vertical. $f.R=I\alpha \\ mg-Ncos\theta -fsin\theta =ma_{ 1 }\\ Nsin\theta -fcos\theta =ma_{ 2 }\\ \\ Equating\quad the\quad acceleration\quad of\quad point\quad of\quad contact\quad on\quad both\quad cylinders:\\ -a_{ 1 }\hat { j } +\quad R\alpha cos\theta \hat { i } +\quad R\alpha sin\theta \hat { j } =\quad a_{ 2 }\hat { i } -\quad R\alpha cos\theta \hat { i } -\quad R\alpha sin\theta \hat { j } \\ \therefore \quad a_{ 2 }=2R\alpha cos\theta \quad And\quad a_{ 1 }=2R\alpha sin\theta \quad \\ On\quad solving\quad a_{ 2 }=\frac { 2gsin\theta cos\theta }{ 3 } \quad ...(1)\\ X\quad co-ordinate\quad of\quad Centre\quad of\quad Bottom\quad cylinder,\quad x\quad =\quad R+2Rsin\theta \\ \therefore \quad dx=2Rcos\theta \quad \dot { \theta } \\ Writing\quad a_{ 2 }\quad as\quad v\quad dv/dx\quad and\quad substituting\quad with\quad dx\quad in\quad (1)\\ \\ v\quad dv\quad =\quad \frac { 4Rgsin\theta \cos ^{ 2 }{ \theta } }{ 3 } d\theta \\ Integration\quad gives\quad us\quad { v }^{ 2 }=\frac { 8gR }{ 9 } (1-\cos ^{ 3 }{ \theta } )\\ Which\quad gives\quad me\quad a\quad different\quad result\quad for\quad maximum\quad velocity.\quad Is\quad this\quad wrong?\quad Why\quad so?\\ Thanks\quad a\quad lot.$

Jatin Sharma - 5 years, 4 months ago

@Deepanshu Gupta – Yes you are right Deepanshu. But with respect to my diagram w1=-w2. This is because according to your diagram angular velocity(w1) is in anti clockwise direction where as I have choose the angular velocity to be in clockwise direction. But you are right that a1=a1.

fig fig

I also want to show how I got w1=-w2

as ${ \alpha }_{ 1 }={ \alpha }_{ 2 }$

so $-\frac { d{ \omega }_{ 1 } }{ dt } =\frac { d{ \omega }_{ 2 } }{ dt }$ (I have added -ve sign because direction of a1 and w1 are opposite to each other)

or $-\int { d{ \omega }_{ 1 } } =\int { d{ \omega }_{ 2 } }$

or ${- \omega }_{ 1 }={ \omega }_{ 2 }+C$

At $t=0$ ${ \omega }_{ 1 }={ \omega }_{ 2 }=0$ So $C=0$

So ${ \omega }_{ 1 }=-{ \omega }_{ 2 }$

What you guys think?

@DEEPANSHU GUPTA @Mvs Saketh

satvik pandey - 6 years, 7 months ago

@Deepanshu Gupta – Yes i got it ,, the fact is that i have represented them as scalars not vectors,, so basically comparing magnitudes,, and i can do that only if i know which is greater,,, i have assumed that rw2 is greater than v2(sin(x)) and so got contradictory results,, got it thanks,,

But this shows that rw2 can never be greater than v2(sin(x)) in the process,,, otherwise we get the contradiction. :)

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – I tried a non energy method and am getting a completely different answer. Can you please help me out by checking my solution?

Jatin Sharma - 5 years, 4 months ago

@Deepanshu Gupta – will this result hold when radius of two cylinder are different?

sashank bonda - 4 years, 6 months ago

@Deepanshu Gupta – @Deepanshu Gupta sir when the radius of two cylinders are different then w1,w2,w(icr) are not same eventhough they form a rigid body

sashank bonda - 4 years, 6 months ago

I think it is correct, absolutely,, correct,, except dont reject theta=0 , at that instant the lower cylinder is actually at rest, only that we already know it was at rest at that instant

Mvs Saketh - 6 years, 7 months ago

why I do not reject $\theta$ = 0 ?? I dont think that it is useful since it gives intial condition in that case it is minimum not maximum so it is useless so I reject it..! Sorry But I can't understand what are you trying to say ? Isn't I make any mistake ?

Deepanshu Gupta - 6 years, 7 months ago

@Deepanshu Gupta – No its not a mistake its not useful surely,, i meant that you rejected pi/2 because it cant exist,, but rejecting 0 along with that makes it appear as if it cant exist either,, :P not that you are wrong or it is useful

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – Okay :)

Deepanshu Gupta - 6 years, 7 months ago

@Deepanshu Gupta – Thank you Deepanshu and Saketh for discussing this question. This discussion is really very useful. Once again thank you guys. :)

satvik pandey - 6 years, 7 months ago

Note- EDITED due to some errors

The situation

Ok so heres the thing, some quick conclusions to draw from observation--

1) The only energy supplier in the system is gravity,

2) That as long as the balls remain in contact , their velocities are constrained, by the relation, ${ v }_{ 1 }tan\theta \quad =\quad { v }_{ 2 }$ where the angle is between the line joining their radii and the normal vertical( v1 for lower ball, v2 for upper ball)

3) For now i am going to assume that the balls remain in contact till the upper ball reaches the floor, we will soon see how this is not true and they depart before that

4)The upper ball only falls vertically because the lower ball only presses it against the wall which offers an equivalent normal reaction for that to happen,

5) Consequently i can say the lower ball only moves horizontally,

Now applying energy conservation ( with potential energy taken 0 at the height of the com of lower sphere) and substituting constraint relation i can say

$mg(2R(1-cos\theta ))\quad =\quad \frac { m{ { v }_{ 1 } }^{ 2 } }{ 2 } +\frac { m{ v }_{ 2 }^{ 2 } }{ 2 } =\frac { m{ { v }_{ 1 } }^{ 2 } }{ 2 } (sec^{ 2 }\theta )$

now using calculus i can show that maxima occurs at theta= arc cos(2/3) degrees (provided i did the calculations correct)

which is * $\sqrt {16 gR /27}$ *

HOWEVER this is where the TWIST occurs,, because if my equations were correct then according to it the speed of the lower ball becomes 0 at angle 90 degrees,, but how is that possible when there is no force acting oppsite to it,, so its velocity can never decrease, so at its maxima or at angle arc cos (2/3) degrees,, the spheres depart and further motion is independent,,

Thus at that angle the two balls get departed,, now you can easily find subsequent velocity of the upper ball as it is free falling under gravity

Now velocity of upper ball at instant of departure is $\sqrt {20 gR /27}$ now individually applying energy conservation for upper ball find velocity max which occurs just before touching ground,,,

*Am i correct @DEEPANSHU GUPTA *

Mvs Saketh - 6 years, 7 months ago

You are done Excellent work!! Hats off!!

But I think final answer should be ${ V }_{ 1,max }=\quad \sqrt { \frac { 16gR }{ 27 } } \\ \\ { V }_{ 2,max }=\quad \sqrt { \frac { 216gR }{ 45 } }$ .

And According to you

$\frac { d{ V }_{ 1 }^{ 2 } }{ d\theta } \quad =\quad 0\\ \\ \quad \theta \quad =\quad 0\quad \quad \times \quad (\quad initial\quad condition\quad )\\ \\ \quad or\quad \\ \quad \quad \theta \quad =\quad \frac { \pi }{ 2 } \quad \quad (\quad rejected\quad )\\ \quad or\quad \\ \boxed { \theta \quad =\quad \cos ^{ -1 }{ \frac { 2 }{ 3 } } }$ .

I'am agreeing with you that the condition

$\theta \quad =\quad \frac { \pi }{ 2 }$ . is rejected because ${ V }_{ 1 }\quad =\quad 0\quad \quad \quad (\because \quad { V }_{ 2 }\quad \neq \quad 0\quad )\quad$ .

which is not possible since lower cylinder never get's stop.

But I have doubt that why does this condition is arouse after differentiation ? Is it coincident or some logic behind it ??

Deepanshu Gupta - 6 years, 7 months ago

Probably because initially the upper cylinder presses the lower cylinder more on the vertical direction and less on the horizontal direction initially ,, so the rate of change of velocity of lower cylinder gradually increases along with velocity,, but slowly as the relative velocity of seperation of the cylinders increase,,, they touch less and less harder with each other till a point where departure happens and further motion cant be treated as a single rigid body system,, funny thing though,, ( i have updated the calculations)

Also @DEEPANSHU GUPTA it is not a coincidence,,, when the derivative of the velocity of lower cylinder becomes 0 , it means its acceleration(except here rate of change with theta and not time, both implie its independence for all future instants) becomes 0 and when does it become 0,, when no force acting on it anymore and when does that happen, when it loses contact with the upper cylinder,, (note acceleration is rate of change with time and not theta obviously,but if velocity becomes constant,, then its derivative with everything becomes 0, which is what i have shown, ofcourse this should happen just once and we should see it as a maxima,,, however through contradiction i have already shown that the cylinders must depart after this instant)

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – Nice solution @Mvs Saketh . The way you gave the mathematical explanation of stuff that why the cylinders loose contact is awesome. Thank you Deepanshu for sharing this problem.

If there would have been friction between the contact contact surface then the cylinders would roll over each other. How should this question be solved?

satvik pandey - 6 years, 7 months ago

@Satvik Pandey – Pandey ji (I am calling you by this name because , I have an friend of similar surname as yours and we call him Pandey ji with love)
I think that will be more interesting and difficult...!! I will surly give a try to it. !!

Deepanshu Gupta - 6 years, 7 months ago

@Deepanshu Gupta – Most of my friends also call me by this name. :D

satvik pandey - 6 years, 7 months ago

@Deepanshu Gupta – fig fig

Now if we apply conservation of energy we have to consider rotational energies also.

I tried to find relation between $\omega$ and $v$

I came up with this equation

${ v }_{ 2 }cos\theta \hat { i } +(r{ \omega }_{ 2 }-{ v }_{ 2 }sin\theta )\hat { j } ={ v }_{ 1 }sin\theta \hat { i } +(r{ \omega }_{ 1 }+{ v }_{ 1 }cos\theta )\hat { j }$

On equating i cap I got ${ v }_{ 2 }={ v }_{ 1 }tan\theta$

and on equating j cap I got $r{ \omega }_{ 2 }-{ v }_{ 2 }sin\theta =r{ \omega }_{ 1 }+{ v }_{ 1 }cos\theta$

or $r{ \omega }_{ 2 }-r{ \omega }_{ 1 }=\frac { { v }_{ 1 } }{ cos\theta }$

Also I think ${ \omega }_{ 2 }={ -\omega }_{ 1 }$ .

@DEEPANSHU GUPTA and @Mvs Saketh , what are you guys getting?

satvik pandey - 6 years, 7 months ago

@Mvs Saketh – yeah...!! Thanks a lot Saketh !!

Deepanshu Gupta - 6 years, 7 months ago

how do I prepare for IPHO

Avieroop Ghosh - 5 years, 8 months ago

HOW do I prepare for ipho? please tell

Avieroop Ghosh - 5 years, 8 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$