Find the Equivalent resistance

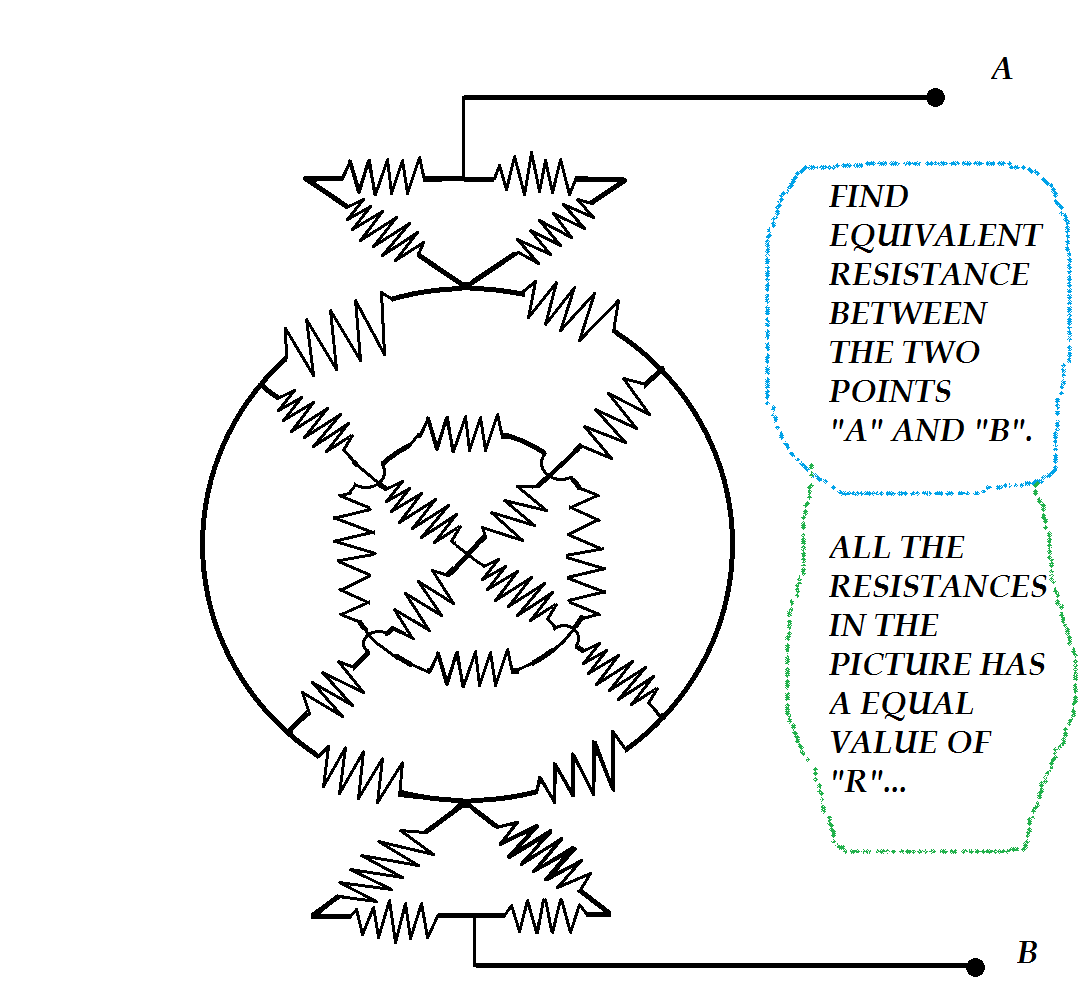
Find the equivalent resistance between the two points a and b.... all the resistances in the picture has equal value of "r".

Take care of the nodes,meshes and branches....please go through the picture in details for better view of the problem.

#Physics #ElectricityAndMagnetism #LearningResources #HelpMe!

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Apply a voltage of $+v$ to point $A$ and $-v$ to point $B$ . The voltage along the horizontal dividing line in the middle is $0 V$ . Now look at the four resistors that connect the outer circle to the inner circle. The outer ends of these four resistors are all at a voltage of $0 V$ . Hence, those four resistors, the four resistors of the inner circle, and the four resistors of the inner cross are all shorted out of the circuit.

Removing those twelve resistors yields a circuit with 3 sections in series, each of which has a resistance of $(R+R) \parallel (R+R) = R$ . Therefore, the total resistance between points $A$ and $B$ is $3R$ .

Jimmy Kariznov - 7 years, 9 months ago

Correct ! Those resistors will get eliminated , as the voltage will remain the same on the wires with no resistance between them . Voting you up !

Priyansh Sangule - 7 years, 9 months ago

aaa aaa

This is the circuit transformation where each resistance are 'r'. If you can't view this image, go to bigger image

Chandreyee Mitra - 7 years, 8 months ago

now I have to convert the star-delta conversion for any one triangle....isn't it?

Sayan Chaudhuri - 7 years, 5 months ago

There are two shortings in this circuit which will not allow any current to flow to the inner branches. Thus, simplifying it we have three resistances in series and thus the answer is 3R.

Rajath Krishna R - 7 years, 9 months ago

the Req of the 2 triangles above and below is R. If you restructure the diagram you will sea that it a wheatstone bridge.So you can eliminate the circuits inside the main circle and evaluate the Req for the outer circle=R. So , the final result will be R+R+R=3R

Jazeel Ameen - 7 years, 9 months ago

Ahhh!!A classical case of 1)WHEATSTONE BRIDGE 2)STAR- DELTA TRANSFORM....

Indraneel Sarkar - 7 years, 9 months ago

The 2 triangles have obviously r as eqln. resistance In case of circle setup inside the circle is shorted. Effectively outer perimeter of circle accounts for resistance and that also comes out to be r. So ++'R'effective=r+r+r=3r++

Harshit Agrawal - 7 years, 9 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$