find the error
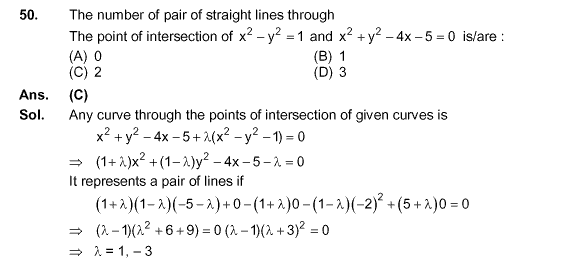
the ans displays here is two but by drawing the figure one can easily point out the ans as 3. what is wrong in this solution
No vote yet
10 votes
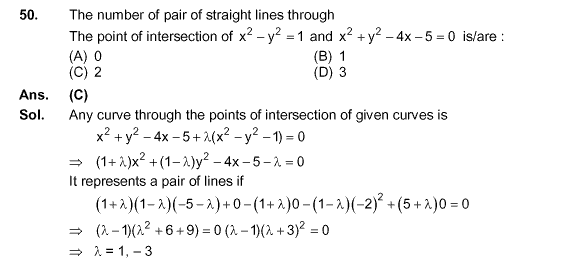
the ans displays here is two but by drawing the figure one can easily point out the ans as 3. what is wrong in this solution
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
λ=-3 has multiplicity of two, so you should write λ = -3, -3
This is a good example of a case where an approach to the problem (in this case algebraic manipulation) results in a different answer than from another approach (Rohitashav used plotting). You should review both methods and try and spot where a mistake was made, and for what reason.
In the case of plotting the points, one can easily see that there are 3 intersection points. Since these points are not collinear, there will be 3 straight lines that can result.
Now, we need to determine what went wrong with the algebraic solution. I can think of several reasons:
1. As Keshav pointed out, λ has a multiplicity, and that might account for additional solutions.
2. Even if λ has a multiplicity of 1, that doesn't necessarily mean that it only corresponds to 1 solution.
3. There could be some flawed reasoning in the steps. What does the first line mean "Any curve through the points of intersection of given curves is f(x,y)+λg(x,y)=0". What does λ seek to measure? How does it correspond to a solution? Is the solution restricted to real values, or complex values (which we'd then have to ignore, as in point 2)?
4. How does "there is a line if ... " follow from the first sentence? How / why did they get rid of all the values of x and y?.
5. Assuming that the logic is valid, does it account for all possible straight lines? Does it allow us to account for lines parallel to the x-axis? How about lines parallel to the y-axis? For example, if λ was to measure the gradient/slope, then it might have issues with infinity.
6. It is entirely possible that the solution is meaningless, as the steps have nothing to do with the problem. Is that the case here? Does it even talk about what the points of intersection are? Shouldn't it only occur when f(x,y)=g(x,y), i.e. when λ=1?
7. Are there calculation errors made in the solution?
I'm not going to spoon feed you, so work through the solution and question everything. I've given you some areas to consider. There might be more.
The no. of straight lines is 3 so no. of pairs will be (23)=3
Log in to reply
yes ,u r correct ,but my ques . is what is the error in the above discussion
Log in to reply
maybe the solution is wrong? as displayed here
when you solve these equation you get value of lemda as 1,-3,-3 so three point of intersection
if we solve both the equations given, and find the value of x to be 3, -1 but from the first equation x^2 = 1+y^2 =>x = sqrt(1+y^2) so when x = -1, we get -1 = sqrt(1+y^2) this is not possible..bcoz ny sqrroot function is defined only for real values of x... so we neglect this solution
and when x = 3 we get 3 = sqrt(1+y^2) which has a got a real value of y...
hence we ignore the values -1
your ans is correct. only two lines are intersecting. the 1st equation is the equation of standard hyperbola so that will not give any line. that will give u a curve and the second equation will give u two intersecting lines