Find the smallest possible inradius

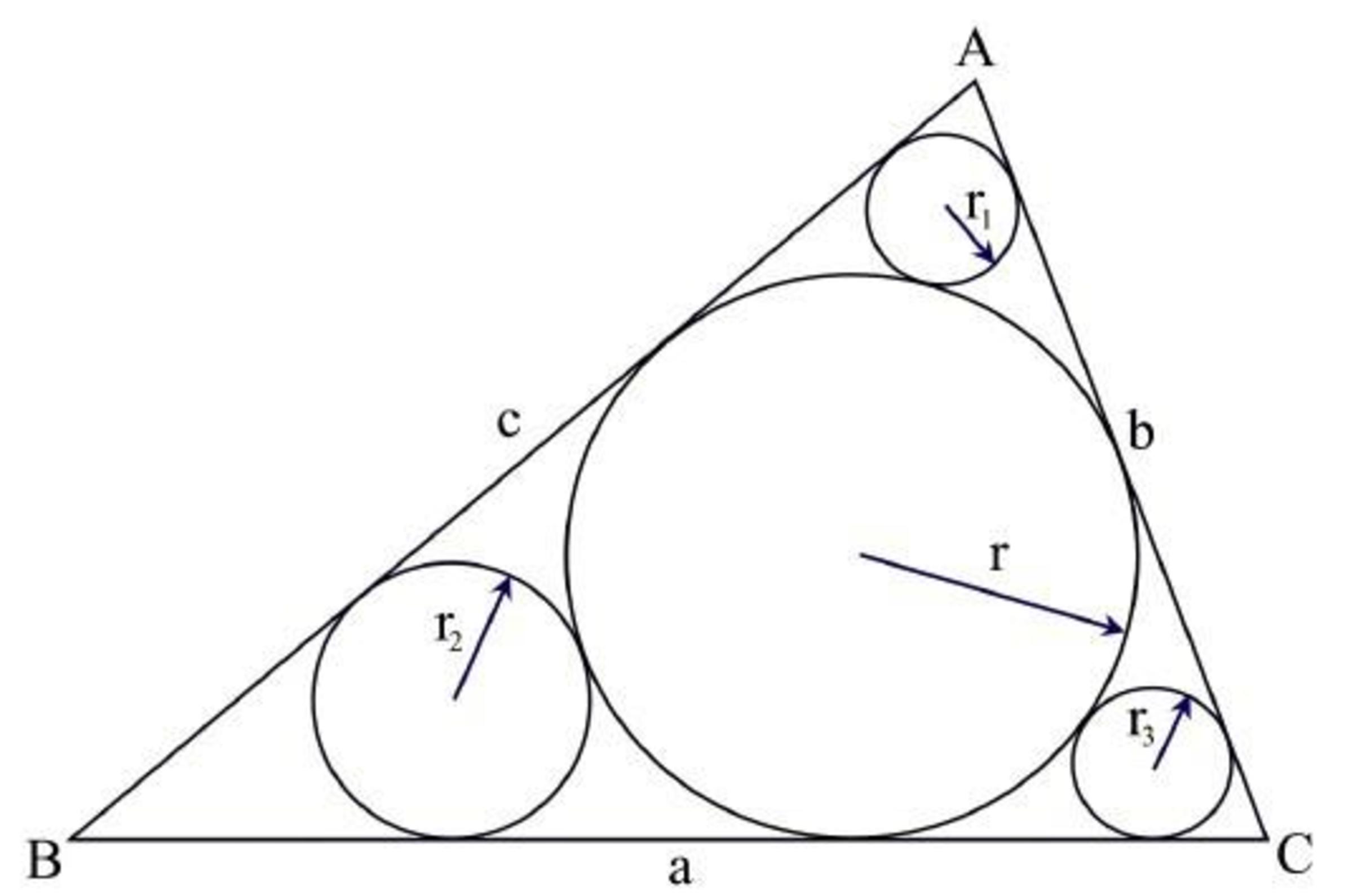
Inside triangle ABC there are three circles with radii $r_1$, $r_2$, and $r_3$. Each is tangent to two sides of the triangle and to its incircle. The incircle has radius $r$. All of $r$, $r_1$, $r_2$, and $r_3$ are distinct perfect square integers. Find the smallest possible value of inradius $r$.

I hope you enjoy this problem.

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

r = 81, r1 = 9, r2 = 36, r3 = 49 is valid, and is probably the smallest possible value (pending some checks on the smaller cases) , by some trigonometric/algebraic arguments.

Letting r, r1, r2, r3 be x^2, a^2, b^2, c^2 respectively, you can force out x^2 = ab + bc + ca; that's all i'll let on

edit: these a,b,c are different from the diagram. (the a,b,c in there are irrelevant). To make it clearer:

r^2 = rt(r1r2) + rt(r2r3) + rt(r3*r1)

Gabriel Wong - 8 years, 1 month ago

Is it that r=81, r1=16, r2=36, r3=49??

Shourya Pandey - 8 years, 1 month ago

1/r=1/r1+1/r2+1/r3

Jet Herng Chion - 8 years, 1 month ago

Hmm.. Gabriel. If r = 81, r1= 9, r2 = 36, and r3 = 49 and by your post: r = x^2 r1 = a^2 r2 = b^2 and r3 =c^2. Wouldn't that make each of the other variables (x, a, b, and c) be the smallest values? As in 81 = x^2 so x = 9, 9= a^2 so a =3, 36 = b^2 so be = 6, and 49 = c^2 so c= 7. With that would those be the new smallest values? Also by looking at the picture we can say that r1 and r3 are the same because the triangle is isosceles. In that case is r1 = 9, r3 = 9... And a and c = 3? So if they were not the same, Plugging the numbers in fit a b and c (3,6,7) we can find the angles of each side. So A = 60.038 B = 92.729 and C = 27.271. From there you can go deeper and find the arc length then find the true radius of each...? I may have done something wrong but, this is just my inquiry for this question.

Nathan Antwi - 8 years, 1 month ago

x^2 = ab + bc + ca

81 = 36 + 67 + 7*3

but this does not imply

x = rt(ab) + rt(bc) + rt(ca)

rt(18) + rt(42) + rt(21) does not equal 9

Gabriel Wong - 8 years, 1 month ago

Is it about Descarte's Theorem?

Andrias Meisyal - 8 years, 1 month ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$