Finding Area

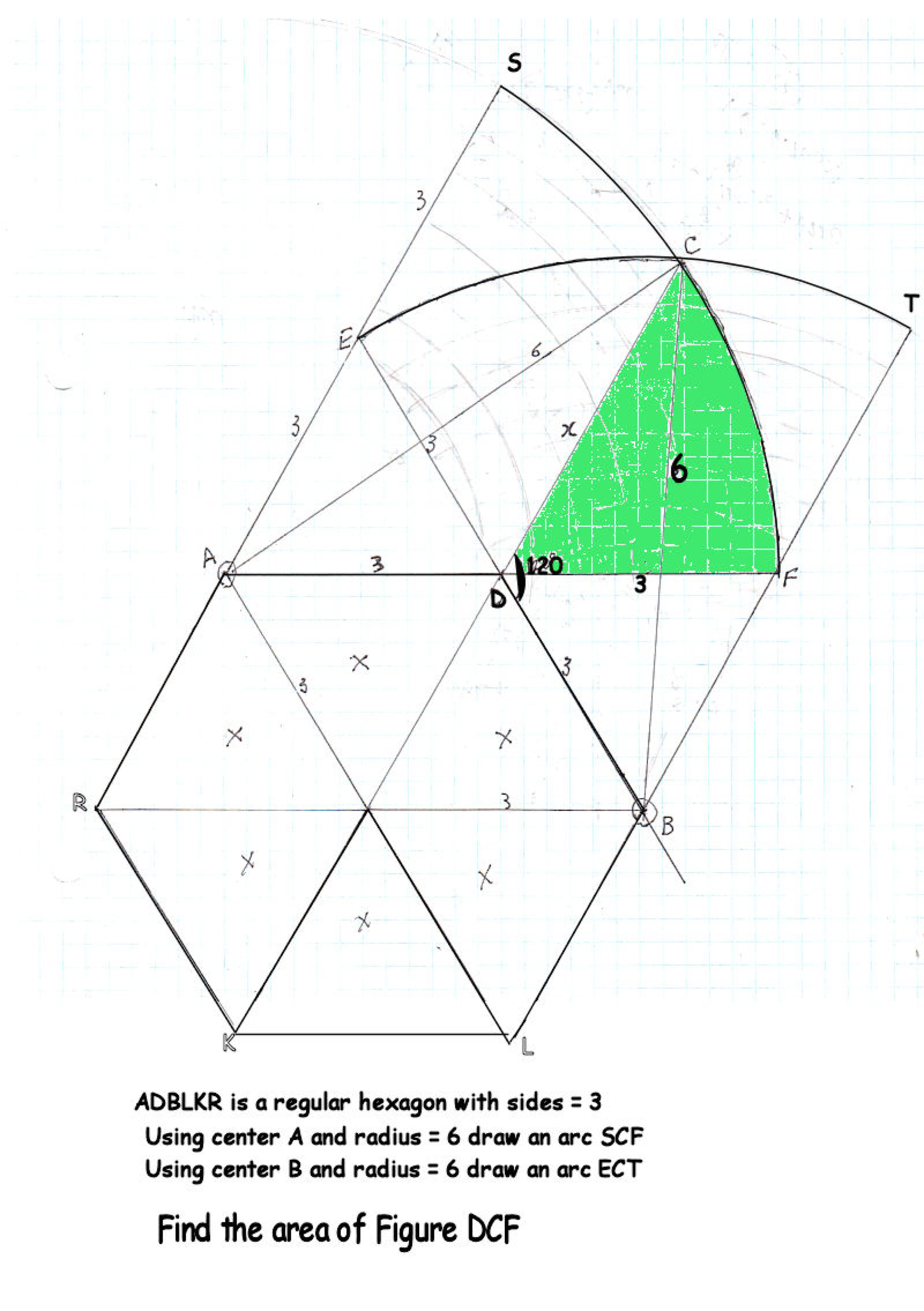
I posted a problem "How Much Can a Goat Eat #2". Using a false assumption I calculated the overlapped area incorrectly. I request assistance in this regard. Please calculate the area of the green colored figure in this image. Thanks.

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

It looks like there are several ways to go about this, but this is my initial thought. First, we have $AB = 3\sqrt{3}$ . Thus $\theta = \angle CAD = \cos^{-1}(\frac{\sqrt{3}}{4}) - \frac{\pi}{6}$ . The area of the green region will then be the area of sector $CAF$ minus the area of $\Delta CAD$ . This comes out to

$(\frac{1}{2})(6^{2})\theta - (\frac{1}{2})(3)(6\sin(\theta)) = 18\theta - 9\sin(\theta)$ .

This "simplifies" to

$18\cos^{-1}(\frac{\sqrt{3}}{4}) - 3\pi - (\frac{9}{8})\sqrt{3}(\sqrt{13} - 1)$ ,

which equals $5.7115$ to $4$ decimal places.

Brian Charlesworth - 6 years, 7 months ago

Thanks, Brian. I obtained the same answer by using a different method. In the sector ACF I calculated A by Law of Sines to be 34.34109373 degrees, altitude from AC to D to be 1.692355197.

Area of the green = Area of the sector - Area of triangle ADC

Area of the green = (34.34.../360 * Pi * 6^2) - (1/2 * 6* 1.69..)

Area of the green = 10.788573 - 5.0770656 = 5.7115074

This amount was taken to the problem "How Much Can a Goat Eat #2" and a corrected answer was obtained.

Guiseppi Butel - 6 years, 7 months ago

Glad we came to the same conclusion. I enjoyed the goat problem; thanks for posting it. :)

Brian Charlesworth - 6 years, 7 months ago

yup its a good sum

Anunoy Chakraborty - 6 years, 7 months ago

wow

Alleria Windrunner Gomez - 6 years, 7 months ago

5.711

Amardeep Singh - 6 years, 7 months ago

Yup got 5.711

Mohit Ahuja - 6 years, 7 months ago

Rohit Dhiman - 6 years, 7 months ago

4.92 square units

Tony Sharma - 6 years, 7 months ago

The area is 8.58

Mohammed El-Sayed - 6 years, 7 months ago

How did you get that answer?

Guiseppi Butel - 6 years, 7 months ago

it can be solved by using integration in a very easy manner .just shift the whole diagram on a xy plane and do the integration by writing the equation .

Shubham Kumar Sah Sah - 6 years, 7 months ago

5.748

Mithun Mehedi Hasan - 6 years, 7 months ago

5.7115 Where did you err?

Guiseppi Butel - 6 years, 7 months ago

what is the correct answer of this problem ????

Deepali shankar - 6 years, 6 months ago

Look back at what Brian and I posted on Oct. 20.

If you think that you have the correct answer please submit your calculations.

Guiseppi Butel - 6 years, 6 months ago

as i tried to solve it i got 4.9 as area of shaded region

Deepali shankar - 6 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$