Finite 3D chessboard

While I was thinking about this problem, I got an idea: what if the board wasn't flat, but instead spherical? Or cube-shaped? After some trial and error, I was able to come up with answers, and I was able to find one cube-shaped board that seemed to work. Here is the design of the cube:

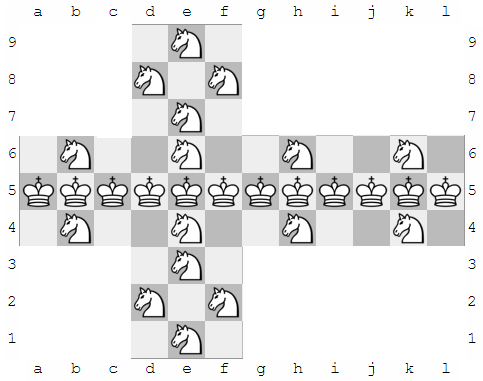
If you've ever folded a cube, you know how these designs can get turned into cubes. The folds should go between c & d, between f & g, between i & j, between 7 & 6, and between 4 & 3.

Here is how the pieces move:

All the kings attack all squares that are adjacent to them.

As an example, the king on c5 attacks the squares b6, b5, b4, c6, c4, d6, d5, and d4. The fold between c and d doesn't hinder the movement.

Another example: the king on a5 attacks the squares a6, a4, b6, b5, b4, l6, l5, and l4. The squares in column l become accessible after folding the cube.

The movements of the knights is like this: they move two steps in one direction, and then 1 step in a perpendicular direction.

As an example, the knight on e6 attacks the following squares: d8, f8, f7, g5, f4, d4, c5, and d7. The squares f7 and d7 are the least obvious. To reach f7, the knight first moves two steps to the right, to g6. Then it moves up to f7. It attacks 2 knights and 2 kings: the knights are on d8 and f8. The kings are on c5 and g5.

Another example: the knight on e7 attacks the following squares: d9, f9, f7, g5, f4, d4, c5, and d7. It attacks 2 knights and 2 kings. The knights are on d8 and f8. The kings are on g5 and c5.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I should add Sizheng Chen posted a solution on a torus when we ran the infinite version of the problem for Problem of the Week.

Jason Dyer Staff - 3 years, 6 months ago

Oh... I wasn't first with coming up with an idea like this...

Stefan van der Waal - 3 years, 6 months ago

The cube is new!

@Jason Dyer – The cube idea is very innovative and the solution is quite elegant! I do have a small technical concern regarding the moves for the knights though (just as a general rule in case if we are to explore other cube solutions): as described, this is based on moving two steps in one direction then one step in a perpendicular direction. As a result, the knight on e6 attacks d7 and f7. However, if the knight moves one step in one direction then two steps in a perpendicular direction, the e6 knight would attack c6 and g6 instead. In fact, according to FIDE, "the knight may move to one of the squares nearest to that on which it stands but not on the same rank, file or diagonal." That would make all of d7, f7, c6 and g6 not accessible for the e6 knight. This situation seems to only apply to knights at the corners and the spaces directly adjacent to the corners (not diagonally adjacent), and by no means affect this nice solution.

Sizheng Chen - 3 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$