Follow-Up to "Pressure Profile"

I posted a problem called Pressure Profile a few days ago. When I wrote the problem, I assumed that when you push on a box without causing it to slide (there is friction), the normal reaction pressure varies linearly with the position along the box.

And sure enough, you can uniquely solve for a linear pressure profile which maintains the box in stasis. This is done by writing and solving two equations which describe the conditions for stasis (2 equations and 2 unknowns).

I then wondered what would happen if we assumed a quadratic pressure variation of the form $P(x) = \alpha x^{2} + \beta x + \gamma$. Now there are three unknown parameters, but still only two equations. I've found that if you simply choose the $\gamma$ parameter and solve for the other two, you can easily come up with a quadratic profile which has the following properties:

1) Satisfies the two equations for stasis
2) Results in positive upward pressure for all values of x between 0 and L

And there are presumably infinitely many such solutions, since I've already just casually found three quadratic profiles that have the above two properties. I suppose it would be possible to find solutions of even higher order as well (5th, 11th, 27th, etc.).

So my questions are these:

1) In the real world, would the pressure profile indeed be linear, as I originally assumed when posting the problem?

2) If so, how does nature know not to choose any higher-order variations in the pressure, since they appear to work, as far as I can tell?

3) Is there another constraint that forces a linear variation that I have simply not considered?

Appendix

For reference, here's the derivation for the general quadratic pressure profile, of which a linear profile is a special case.

$dA = W dx$ $P(x) = \alpha x^{2} + \beta x + \gamma$ $dF = P dA$ $d\tau = Px dA$

$Force: \frac{Mg}{W} = \int_{0}^{L} (\alpha x^{2} + \beta x + \gamma) dx \\ \implies \frac{Mg}{W} = \alpha \frac{L^3}{3} + \beta \frac{L^2}{2} + \gamma L$

$Torque \, about \, (0,0): \frac{Mg}{W} \frac{L}{2} + \frac{F}{W} \frac{H}{2} = \int_{0}^{L} (\alpha x^{3} + \beta x^{2} + \gamma x) dx \\ \implies \frac{Mg}{W} \frac{L}{2} + \frac{F}{W} \frac{H}{2} = \alpha \frac{L^4}{4} + \beta \frac{L^3}{3} + \gamma \frac{L^2}{2}$

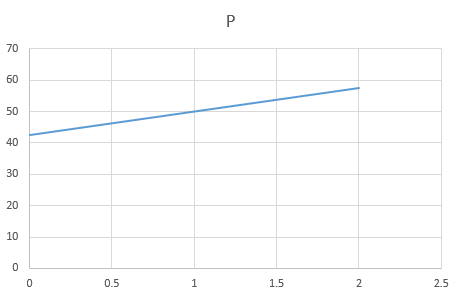
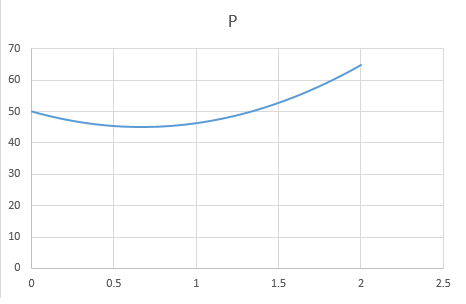
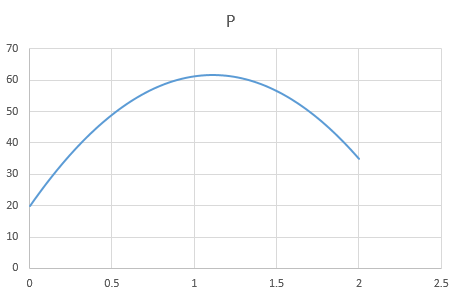
By choosing the $\gamma$ parameter and solving the two equations for $\alpha$ and $\beta$, we can generate numerous quadratic solutions. By setting $\alpha$ to zero and solving for the other two, we can uniquely generate a linear profile. Here are three example profiles that seem to work (pressure is positive between 0 and L and the two equations for stasis are satisfied):

1) $\alpha = 0,\beta = 7.5,\gamma = 42.5$

2) $\alpha = 11.25,\beta = -15.0,\gamma = 50.0$

3) $\alpha = -33.75,\beta = 75.0,\gamma = 20.0$