Force Between Two "Short" Current-Carrying Wires

In attempting to solve a community problem posted recently, I derived a formula for the magnetic force between two current-carrying wire segments of arbitrary length (but same for both) and arbitrary spacing. These may well be parts of infinite line segments, but the formula only accounts for the interactions between the two finite segments. The derivation is rather tedious, so I won't post it right now:

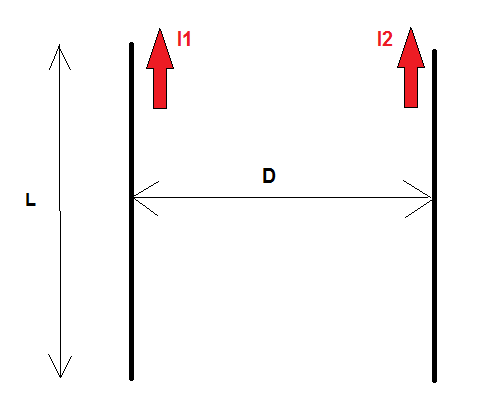
The formula ends up being:

$F = \frac{\mu_0 I_1 I_2}{2 \pi} \Big ( \frac{\sqrt{D^2 + L^2}}{D} -1 \Big )$

For conductor length much larger than the spacing, the result reduces to:

$F \approx \frac{\mu_0 I_1 I_2}{2 \pi} \frac{L}{D}$

The second formula is the well-known expression for the force between two long wires, so that's a good sign. I have also confirmed the result with numerical simulations.

Does anybody else know off the top of their head that this is correct?

#ElectricityAndMagnetism

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Laszlo Mihaly @Ashish Siva What do you think?

Steven Chase - 3 years ago

yes, I attempted the derivation and obtained the same result. Musn't be a coincidence. ;)

Ashish Menon - 3 years ago

I would calculate the vector potential ( easier than Biot Savart), take the gradient and integrate the force over the length of the other wire. Too busy with real work to do it.

Laszlo Mihaly - 3 years ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$