Four points in a square!

Given arbitrary $3$ points $A,B,C$ , can we construct (only using compass and straightedge) an equilateral triangle $\triangle PQR$ such that $A, B, C$ lie on the sides of $\triangle PQR$ ?

Yes, we can! Try it for yourself before reading on.

We use the following sequence of steps:

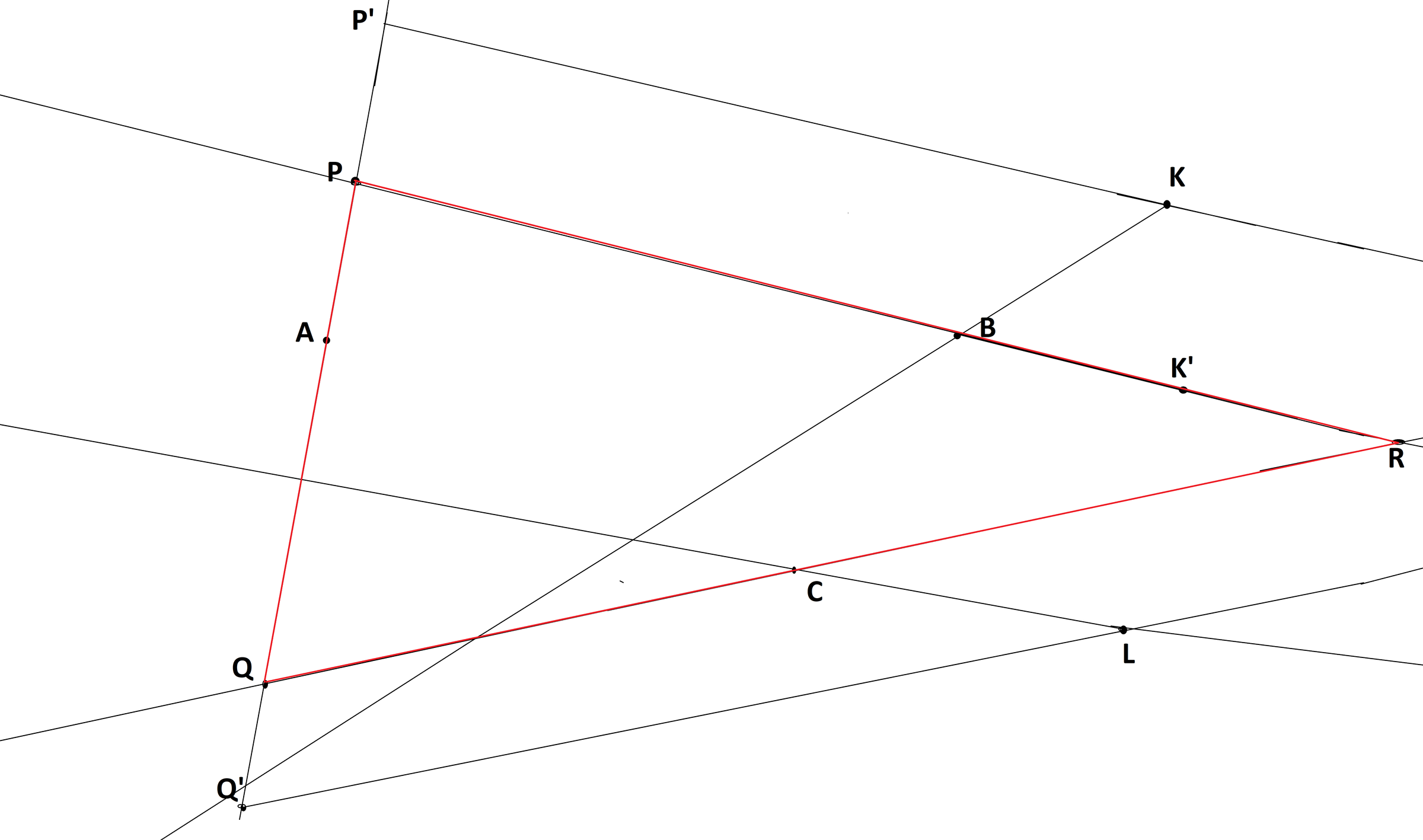
Draw a arbitrary line from point $A$ not touching point $B$ and $C$
Take an arbitrary point $P'$ on the line and draw another line from $P'$ till $K$ such that $\angle AP'K=60^\degree$ (see how to draw $60^\degree$ with compass here)
Join $K$ and $B$
Extend a line from $B$ till $K'$ such that $\angle P'KB=\angle KBK'$ (see how to draw)
Extend $\overline{BK'}$ intersecting $\overline{AP'}$ at $P$
As in step $2$ draw angle $\angle PQ'L=60^\degree$
As in step $3$ join $L$ and $C$
As in step $4$ Draw line $\overline{CQ}$
Extend $\overline{PB}$ and $\overline{QC}$ and let them intersect at $R$
Now points $A,B$ and $C$ lie on the sides of the equilateral triangle $\triangle PQR$

Justification:

After step $4$ $\angle P'KB=\angle KBK'$ $\Rightarrow \overline{P'K} \parallel \overline{PR}$ $\Rightarrow \angle QPR=\angle QP'K$ As from step $2$ $\angle QP'K=60^\degree$ $\Rightarrow QPR=60^\degree........[1]$ Similarly we can prove that $\angle PQR=60^\degree.......[2]$ From angle sum property of triangle $\angle PRQ=60^\degree........[3]$ From $[1],[2]$ and $[3]$ it is proved that $\triangle PQR$ is an equilateral triangle

Now a bonus : Given arbitrary points $A,B,C$ and $D$ can you draw a square $PQRS$ such that points $A,B,C$ and $D$ lies on the sides $\overline{PQ},\overline{QR},\overline{RS},\overline{SP}$ - A problem given by Jeff Giff

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Hyper-Brilliant!

@Zakir Husain

Yajat Shamji - 11 months, 2 weeks ago

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Jeff Giff - I didn't write my construction for rectangle (it will take more time and lines which I don't have this time! )

Zakir Husain - 11 months, 2 weeks ago

@Yajat Shamji, @Kumudesh Ghosh, @Kriti Kamal, @Aryan Sanghi, @Vinayak Srivastava, @Mahdi Raza, @Alak Bhattacharya, @Marvin Kalngan

Are you allowed to extend a side of the square beyond the segment between the vertices? If not, then if A,B,C are the vertices of an equilateral triangle and D is the centre of the triangle, no square can be constructed.

Justin Travers - 11 months, 2 weeks ago

@Justin Travers - If $A,B,C$ and $D$ forms a concave quadrilateral then no rectangle can be constructed, and as a square is a rectangle also therefore if $A,B,C$ and $D$ forms a concave quadrilateral then the square we desired is not possible. Therefore $A,B,C$ and $D$ must form a convex quadrilateral together.

@Zakir Husain Yes,for concave quadrilateral no rectangle can be drawn.Can you recommend me some books for geometry??Thanks in advance

A Former Brilliant Member - 11 months, 2 weeks ago

@A Former Brilliant Member – I myself don't use any book for geometry, what I will recommend is to practice yourself. It will help a lot

@Zakir Husain – Thanks

I will try to give a method of the Bonus Question, though I think it can be simplfied.

Construct circles with diameter $AC$ , $BD$ , and call them $\omega_A$ , $\omega_B$ , respectively.

Construct circles with the same radius $r$ centered at A and B, call them $O_A,O_B$ , respectively.

The radical axes of $O_A$ and $\omega_A$ is $L_A$ , and define $L_B$ similarly.

Construct a circle with diameter $AB$ , call it $\Omega$ , and its center $M$ .

Choose $K$ on $\Omega$ such that $KA=KB$ .

$KA$ intersects $L_A$ at $E$ , $F$ is on $KM$ such that $FE\perp EK$ .

The circle with diameter $KF$ intersects $L_A$ at point $G$ other than $E$ .

$H$ is on $L_B$ such that $HG\perp GE$ , and $BH$ intersect $\Omega$ at a point $I$ other than $B$ .

Reflect $I$ about $M$ and we get $Q$ .

X X - 11 months, 2 weeks ago

About what radius $r$ do you mean in the second step?

You can choose any length to be the radius, just make sure the two circles are the same size.

Can you also give a justification or proof that how these steps work so that the answer becomes mathematically acceptable

I used inversion, Steiner Conic, and spiral similarity to come up with this. I will try to figure out if there is a simpler proof for this construction.

Second attempt:) (Much simpler)

Call the circle with diameter $AB$ $\Omega$ . Choose $K$ on $\Omega$ such that $KA=KB$ .

$AC$ intersect $\Omega$ at point $E$ other than $A$ , and construct the circumcircle of $CEK$ , call it $\omega$ .

$\omega$ intersects the circle with diameter $CD$ at a point other than $C$ , which is the desired $S$ .

There are two choices of $K$ , so there are two squares that satisfies the condition.

Can you please give a proof or justification also for your steps of construction?

I will give an idea of how I come up with this construction.

First of all, let the foot of $A$ , $B$ on $RS$ , $SP$ be $A'$ , $B'$ , respectively.

We know that $A',B'$ lie on the circle with diameter $AC,BD$ , respectively.

Also, we have $AA'=BB'$ , and $AA'\perp BB'$ , thus the intersection of $AA'$ and $BB'$ lies on $\Omega$ .

We now know that the Miquel point( $K$ ) of complete quadrilateral $AA'B'B$ is on $\Omega$ , and since $AA'=BB'$ , we have $KA=KB$ (thus the location of K), and $KA'=KB'$ .

Hence the goal is to find two points $A',B'$ , which lie on the circle with diameter $AC,BD$ , respectively, and satisfies $KA'=KB'$ and $KA'\perp KB'$ .

So actually $B'$ is the point obtained by rotating $A'$ around $K$ for $90^{\circ}$ , hence we rotate all the possible location of $A'$ , which is the circle with diameter $AC$ , around $K$ for $90^{\circ}$ .

Let $C'$ be the point obtained by rotating $C$ around $K$ for $90^{\circ}$ , then the circle we obtained on the previous step has diameter $BC'$ , so $B'$ lies on both the circle with diameter $BC'$ and the circle with diameter $BD$ .

So it is the matter of how to find $C'$ . Since the Miquel point of $ACC'B$ is also $K$ , the intersection of $AC$ and $BC'$ lies on $\Omega$ , which is $E$ .

According to the above, $C'$ lies on the circumcircle of $CEK(\omega)$ . Also $CC'$ is the diameter of $\omega$ since $\angle CKC'$ is a right angle.

Since $B'$ lies on both the circle with diameter $BC'$ and the circle with diameter $BD$ , $BB'$ is the radical axes of the two circles, so $BB'$ is perpendicular to $C'D$ .

Also, $SC// BB'$ , so $SC\perp C'D$ . We have $CS\perp DS$ , so $C',D,S$ are collinear, hence $\angle CSD=\angle CSC'=90^{\circ}$ , which leads to $S$ lying on $\omega$ .

We have that $S$ lies on $\omega$ , and also $S$ lies on the circle of diameter $CD$ , hence the construction.

@X X – This is how I thought of the construction, a bit long, but perhaps there is a simpler explanation or proof of why this construction works.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$