Framing on R.....Can my truck pass through this tunnel?

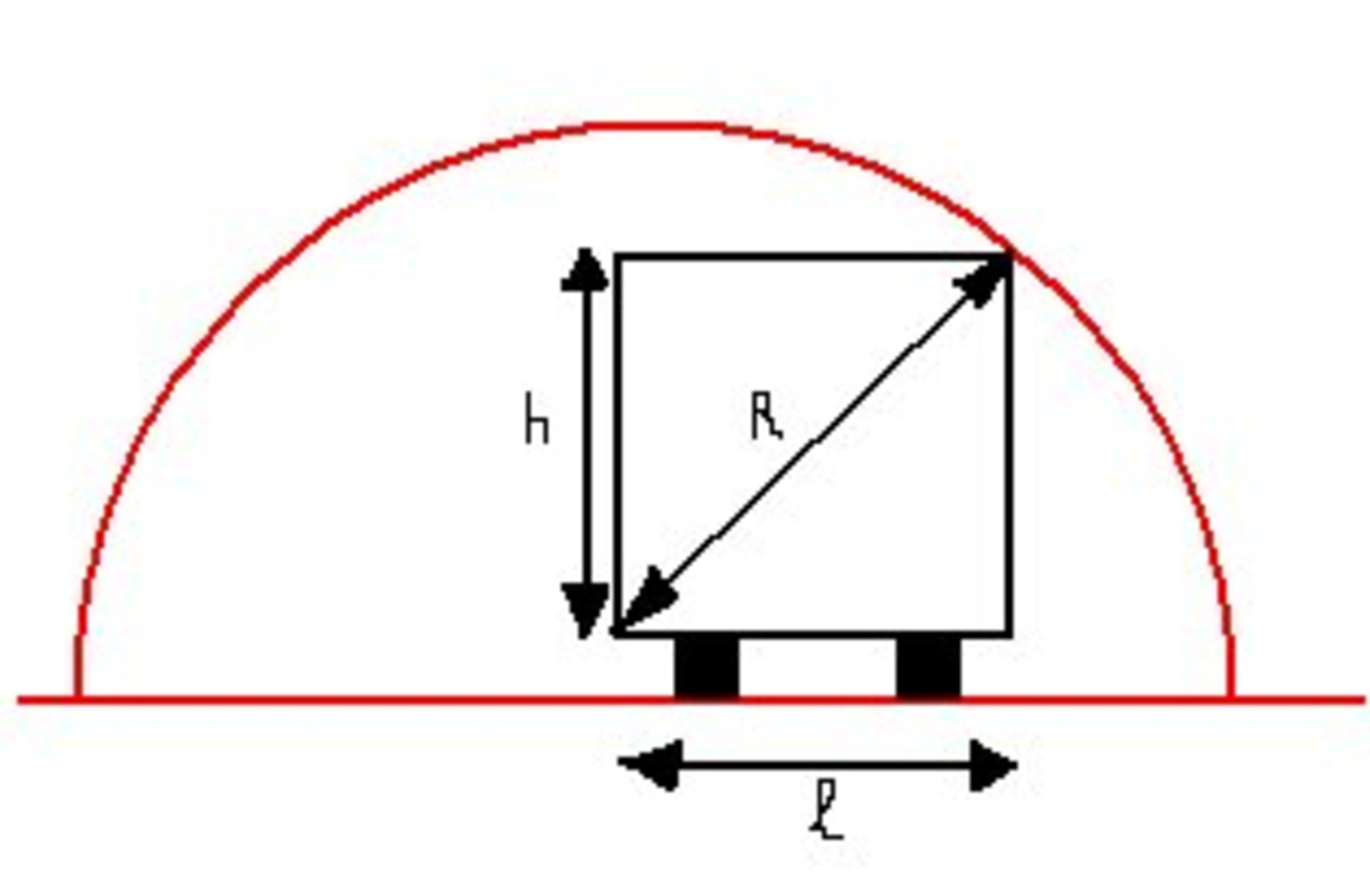
A tunnel in the form of a semi cylinder has a radius of 4 m. A factory has several trucks whose widths L vary between 2m and 2.40m and whose heights vary between 3.10m and 3.30m.
Can all the trucks pass in this tunnel without exceeding the red line indicated in the figure?
The heights mentioned is from ground to the top of the trucks.

#Geometry #MathProblem #Math

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Do you mean the red lines indicated? Or there are some other blue lines that is not shown?

敬全钟 - 7 years, 6 months ago

Sorry I meant the read line.

Oussama Jaber - 7 years, 6 months ago

The truck with the largest cross-section diagonal is the one with the greatest dimensions; namely, 2.4m x 3.3m. We have that $\sqrt{2.4^2+3.3^2}\approx 4.08$ ; but since the semi-cylinder can only fit up to 4 meters diagonally, not all the trucks can fit.

I am assuming that the truck must occupy one half of the cylinder or less, therefore following driving laws.

Daniel Liu - 7 years, 6 months ago

All I could do is frame both L and h
$2 \leq L \leq 2.40$
$3.10 \leq h \leq 3.30$
What should I do next?

Oussama Jaber - 7 years, 6 months ago

Distance from the center to the circumference stays the same. So, (l/2)^2 + h^2 <= r^2 where r is the radius. I can't figure out the blue line in your picture.

Lokesh Sharma - 7 years, 6 months ago

I meant red line

Oussama Jaber - 7 years, 6 months ago

Is the height of the truck tires significant?

Daniel Liu - 7 years, 6 months ago

The height of the truck mentioned includes the height of the truck. Sorry the picture should be modified so the height line should go all the way to the ground.

Oussama Jaber - 7 years, 6 months ago

i assumed that the truck shouldn't exceed the line halving the tunnel width ,or the tunnel radius . in this case if the maximum height is 3.3 m ,then the maximum width should be 3.3 m also ,because the cross section of the tunnel is a half circle ,so yes all the trucks can pass the tunnel .

Mohamed Mohamed Dehairy - 7 years, 6 months ago

$=\quad \{ (l,\quad h):\quad \frac { { l }^{ 2 } }{ 4 } +{ h }^{ 2 }\le { R }^{ 2 },\quad 2\le l\le 2.40,\quad 3.10\le h\le 3.30\}$

Lokesh Sharma - 7 years, 6 months ago

ALL trucks can pass through the tunnel .Any truck with width 2.4 and height not greater than 3.815... can pass through the tunnel.

SAMARTH M.O. - 7 years, 6 months ago

is it one way or two day road ?

anq anq - 7 years, 6 months ago

one way

Oussama Jaber - 7 years, 6 months ago

have four lanes semi trucks go on the 2 enter lanes even tho its not safe

Curtis Noble - 5 years, 8 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$