Fundamental Theorem of Analysis for discontinous functions

Last week I discovered a very neat property of improper Integrals. There are some functions where it is possible to calculate the area under the curve with the Fundamental Therorem of Analysis even if the function is discontinuous .

Let's say you have a function f(x)f\left( x \right) and you want to calculate ∫abf(x)dx\int _{ a }^{ b }{ f\left( x \right) dx } . But unfortunately there is a pole point at xp{ x }_{ p } with b>xp>ab>{ x }_{ p }>a.Now I will prove that: If xp{ x }_{ p } is the only point on [a;b]\left[ a;b \right] where ff is discontinuos and there exists a point P(xp;yp)P\left( { x }_{ p };{ y }_{ p } \right) to which ff is point symmetric, then it is possible to calculate the integral with the Fundamental Therorem of Analysis.

Because it is an improper integral, you devide the ingral into two: ∫abf(x)dx=lim⁡z→0+(∫axp−zf(x)dx+∫xp+zbf(x)dx)\int _{ a }^{ b }{ f\left( x \right) dx } =\lim _{ z\rightarrow { 0 }^{ + } }{ \left( \int _{ a }^{ { x }_{ p }-z }{ f\left( x \right) dx } +\int _{ { x }_{ p }+z }^{ b }{ f\left( x \right) dx } \right) } Because xp { x }_{ p } is the only point of discontinuity of ff, ff is continous on [a;xp−z]\left[ a;{ x }_{ p }-z \right] and on [xp+z;b]\left[ { x }_{ p }+z;b \right] and therefore you can calculate this with the Fundamental Therorem of Analysis, if FF is the antiderivative of ff: ∫abf(x)dx=lim⁡z→0+(F(xp−z)−F(a)+F(b)−F(xp+z))∫abf(x)dx=F(b)−F(a)+lim⁡z→0+(F(xp−z)−F(xp+z))\begin{aligned} \int _{ a }^{ b }{ f\left( x \right) dx } &= \lim _{ z\rightarrow { 0 }^{ + } }{ \left( F\left( { x }_{ p }-z \right) -F\left( a \right) +F\left( b \right) -F\left( { x }_{ p }+z \right) \right) } \\ \int _{ a }^{ b }{ f\left( x \right) dx } &= F\left( b \right) -F\left( a \right) +\lim _{ z\rightarrow { 0 }^{ + } }{ \left( F\left( { x }_{ p }-z \right) -F\left( { x }_{ p }+z \right) \right) } \end{aligned} If xp{ x }_{ p } is a pole point of ff then it is a pole point of FF as well. ff is point symmetric to P(xp;yp)P\left( { x }_{ p };{ y }_{ p } \right) and because ff is a measure of the slope of FF (because ddxF(x)=f(x)\frac { d }{ dx } F\left( x \right) =f\left( x \right) ), FF must be axially symmetrical to x=xpx={ x }_{ p }.

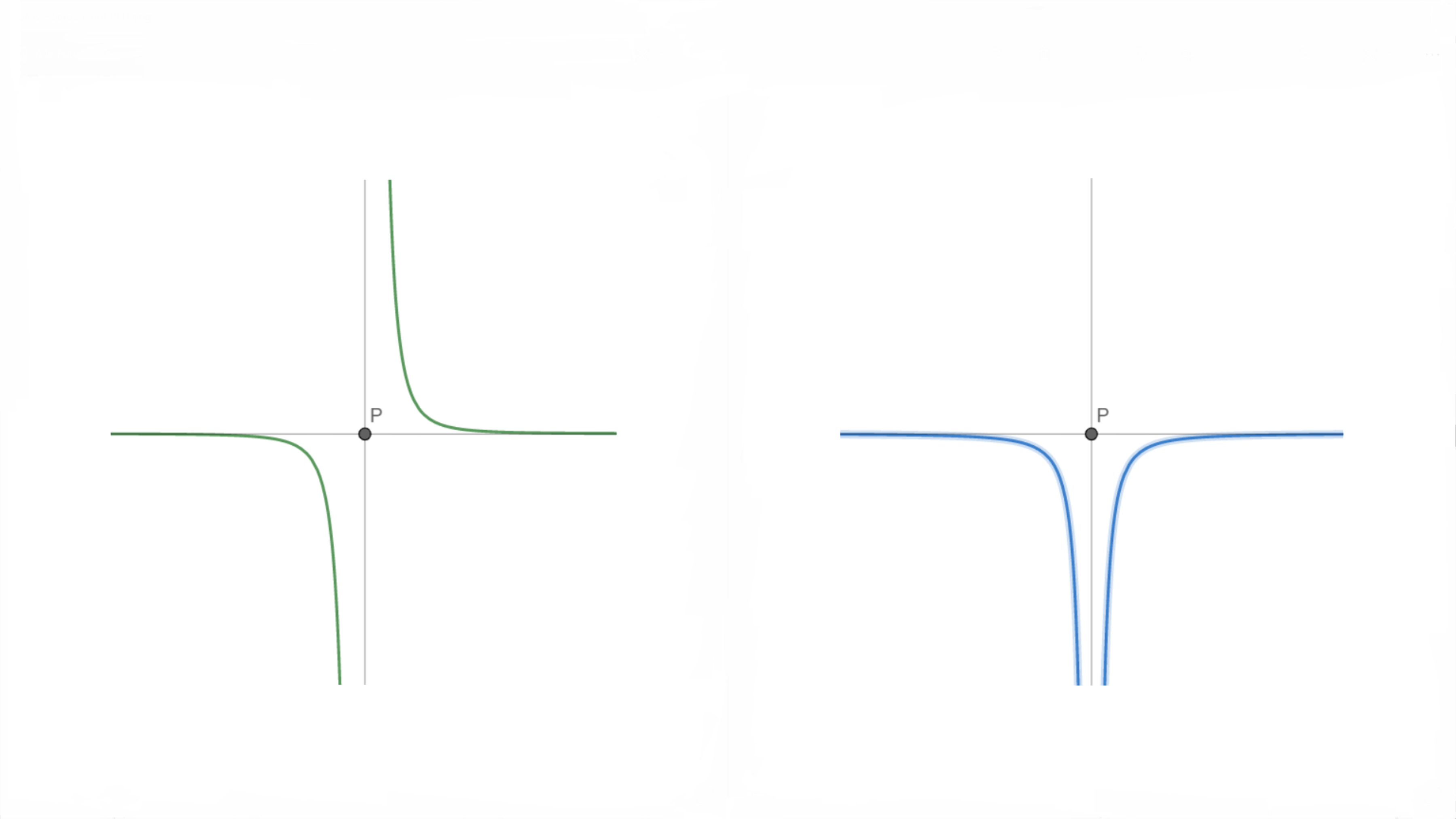an example point symmetric function \(f\) in green and a possible axial symmetrical antiderivative of \(f\) in blue an example point symmetric function ff in green and a possible axial symmetrical antiderivative of ff in blue

And Therefore: F(xp−z)=F(xp+z)F(xp−z)−F(xp+z)=0F\left( { x }_{ p }-z \right) =F\left( { x }_{ p }+z \right) \\ F\left( { x }_{ p }-z \right) -F\left( { x }_{ p }+z \right) =0

∫abf(x)dx=F(b)−F(a)\int _{ a }^{ b }{ f\left( x \right) dx } =F\left( b \right) -F\left( a \right)

The geometric interpretation of this relationship is, that the infinite areas on the left and right side of the pole cancel out each other because of the opposite sign.

It is important to mention, that the antiderivative must be defined for every x≠xpx\neq { x }_{ p } in [a;b]\left[ a;b \right] , because otherwise it will not work.

#Calculus

Note by CodeCrafter 1
1 year, 3 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Edit:

In this proof, I used the argument, that the antiderivative of ff must be axial symmetrical to x=xpx={x}_{p}. But this is not true for all functions.

For example if f(x)=x3+1f \left( x \right) = x^3 + 1 then the antiderivative is F(x)=14x4+xF \left( x \right) = \frac{1}{4} x^4 + x. ff is point symmtric to P(0;1)P \left( 0;1 \right) but FF is not axial symmetrical to x=0x=0. But as we go closer and closer to the pole point, then we approach a "axial symmetry". Therefore near the pole point FF is axially symmetrical and hence the important limit in the proof above still converges to 0.

But unfortunately I cannot find a general argumentation, which guarantees that there are no counterexamples.

CodeCrafter 1 - 1 year, 3 months ago
×

Problem Loading...

Note Loading...

Set Loading...