Futoshiki problem 6 ?p=6

Answer say it needs only two number to have a unique solution. But here is an example where you start with two number, but the third can be defining different possible solution. 2 is not enough for unique solution it appears to me.

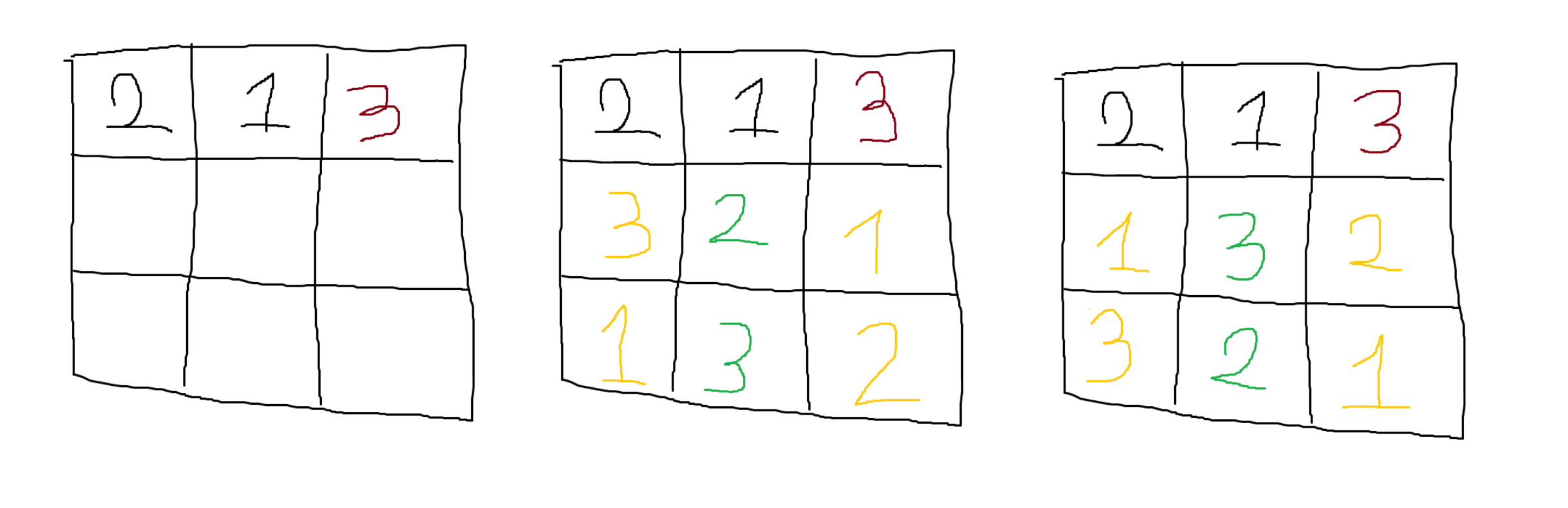
Please let me know if there's something i'm missing or if the solution provided is to be corrected. Thank you very much

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Hi, I believe you're referring to this problem.

the question reads:

What's the minimum number of digits that must be filled in before the puzzle can have a unique solution?

not

What's the minimum number of digits that must be filled in before the puzzle must have a unique solution?

In the future, if you have concerns about a problem's wording/clarity/etc., you can report the problem. See how here.

Brilliant Mathematics Staff - 3 months, 3 weeks ago

The correction says: 2 placements are enough, so long as they are different numbers (and are on different rows and columns).

The answer is 2? Or the answer is 2.. so long, and? If the answer is 2 so long, and.. those conditions should be told before and not after.

Daniel Assayag - 3 months, 2 weeks ago

The problem statement didn't state that you must fill in the same digit. So you're free to use distinct digits.

Brilliant Mathematics Staff - 3 months, 2 weeks ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$