Gauss's Law / Dielectric Boundary

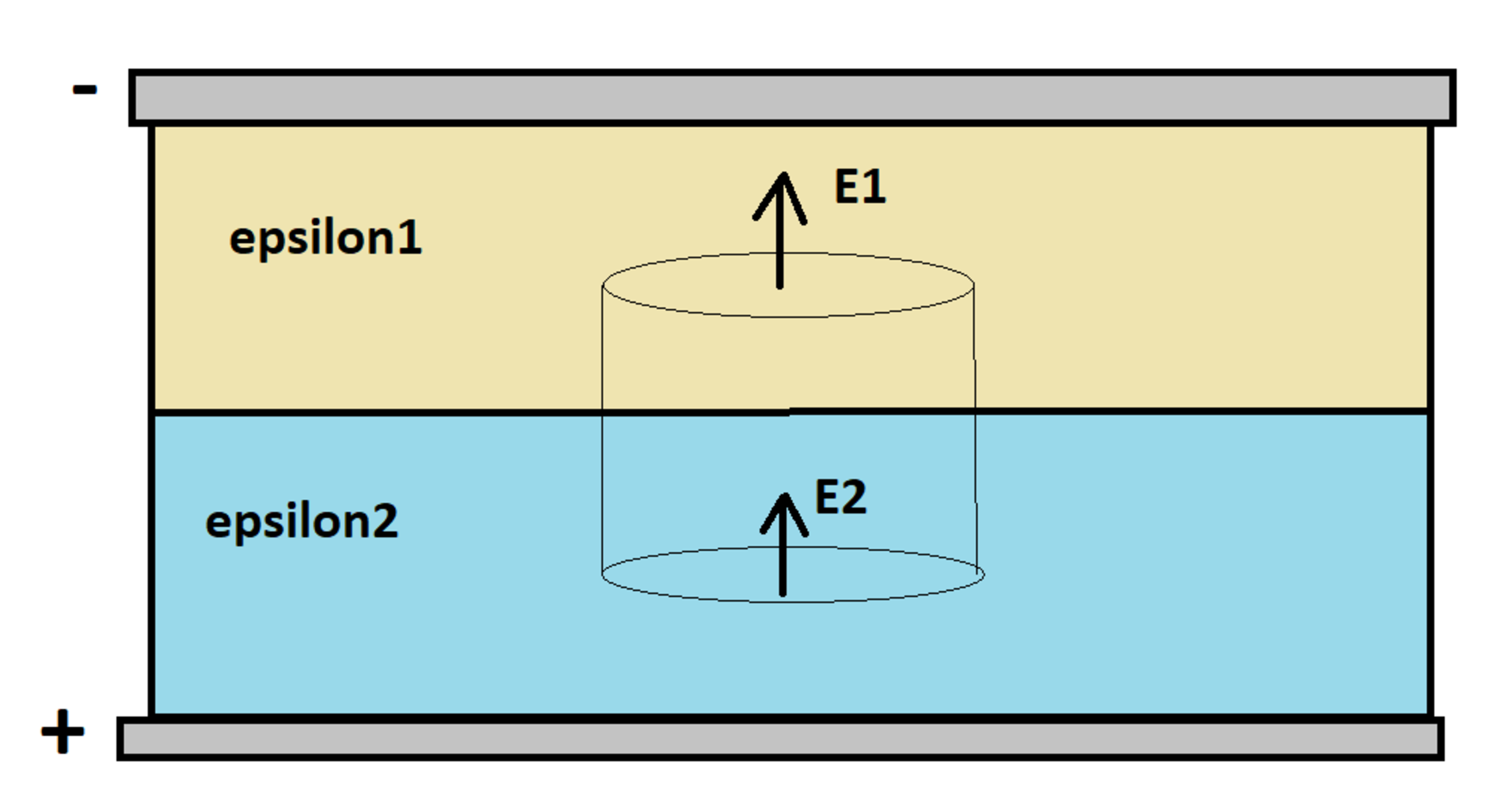
Consider a charged capacitor with two different dielectric materials, as shown. The electric fields point from the positive plate to the negative plate. Determine the relationship between the electric fields $E_1$ and $E_2$ .

Draw a Gaussian surface around the dielectric boundary as shown, and apply Gauss's law to the closed surface.

$\int \int \epsilon \vec{E} \cdot \vec{dS} = Q$

In the above equation, $Q$ is the enclosed free charge at the dielectric interface. In the ordinary "text book" case, $Q = 0$ . Integrating over the top and bottom surfaces results in (assuming the top and bottom surfaces have area $A$ ):

$\epsilon_1 E_1 A - \epsilon_2 E_2 A = 0 \\ \epsilon_1 E_1 = \epsilon_2 E_2$

#ElectricityAndMagnetism

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Talulah Riley I will be traveling most of the day today, so this might be the last thing I post

Steven Chase - 8 months, 1 week ago

@Steven Chase where you are travelling? For your work or chilling your life??

Talulah Riley - 8 months, 1 week ago

@Steven Chase Thanks for the note.

Talulah Riley - 8 months, 1 week ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$