General way to find $\sum _{ x=1 }^{ i }{ { x }^{ n } } ,\quad n\in N$ .

Let $\sum _{ x=1 }^{ i }{ { x }^{ n } } ,\quad n\in N=f(n)$ .

Using the following fact and a bit of working around we can find f(n).

That is, $(1+x)^\alpha = \sum_{k=0}^{\alpha} \binom{\alpha}{k} x^k$ , where $\binom{\alpha}{k} = \frac{\alpha(\alpha-1)\cdots(\alpha-k+1)}{k!}.$

For finding f(n) we must know f(1),f(2),......f(n-1).

The following method illustrates the way to find the sum of 4th power of natural numbers , the same can be used for finding for any nth power.

To try a problem based on this go below.

Adding rectangular areas

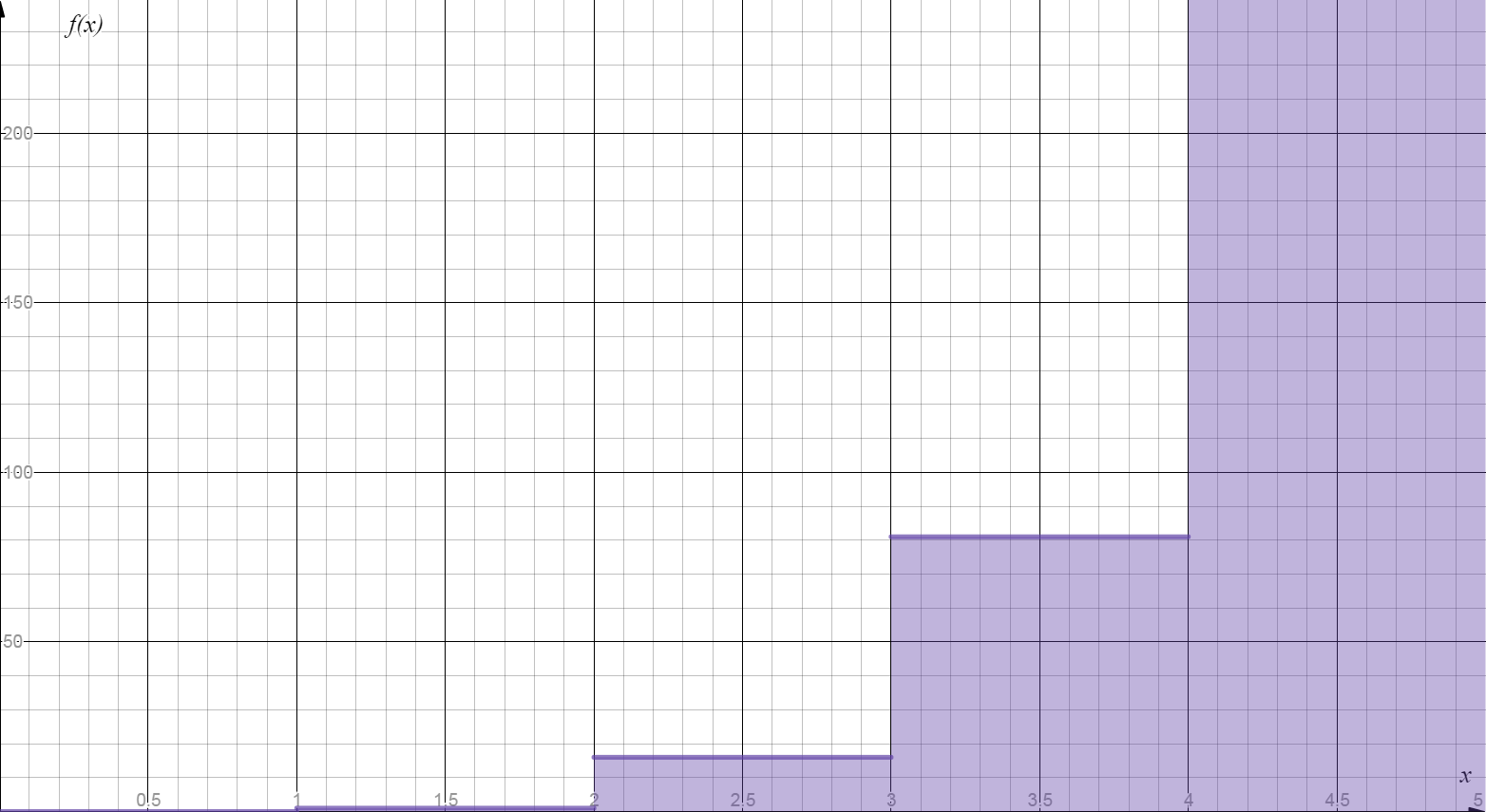
Find the area bounded between $y = \lfloor x\rfloor ^4$ , the $x$ -axis, $x = 0$ and $x=11$ .

Notation: $\lfloor \cdot \rfloor$ denotes the floor function.

#Calculus

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

There's another method also known as Faulhaber's Formula.

Arkajyoti Banerjee - 3 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

General way to find ∑x=1ixn,n∈N\sum _{ x=1 }^{ i }{ { x }^{ n } } ,\quad n\in N∑x=1i​xn,n∈N.