Geometry problem of a triangle

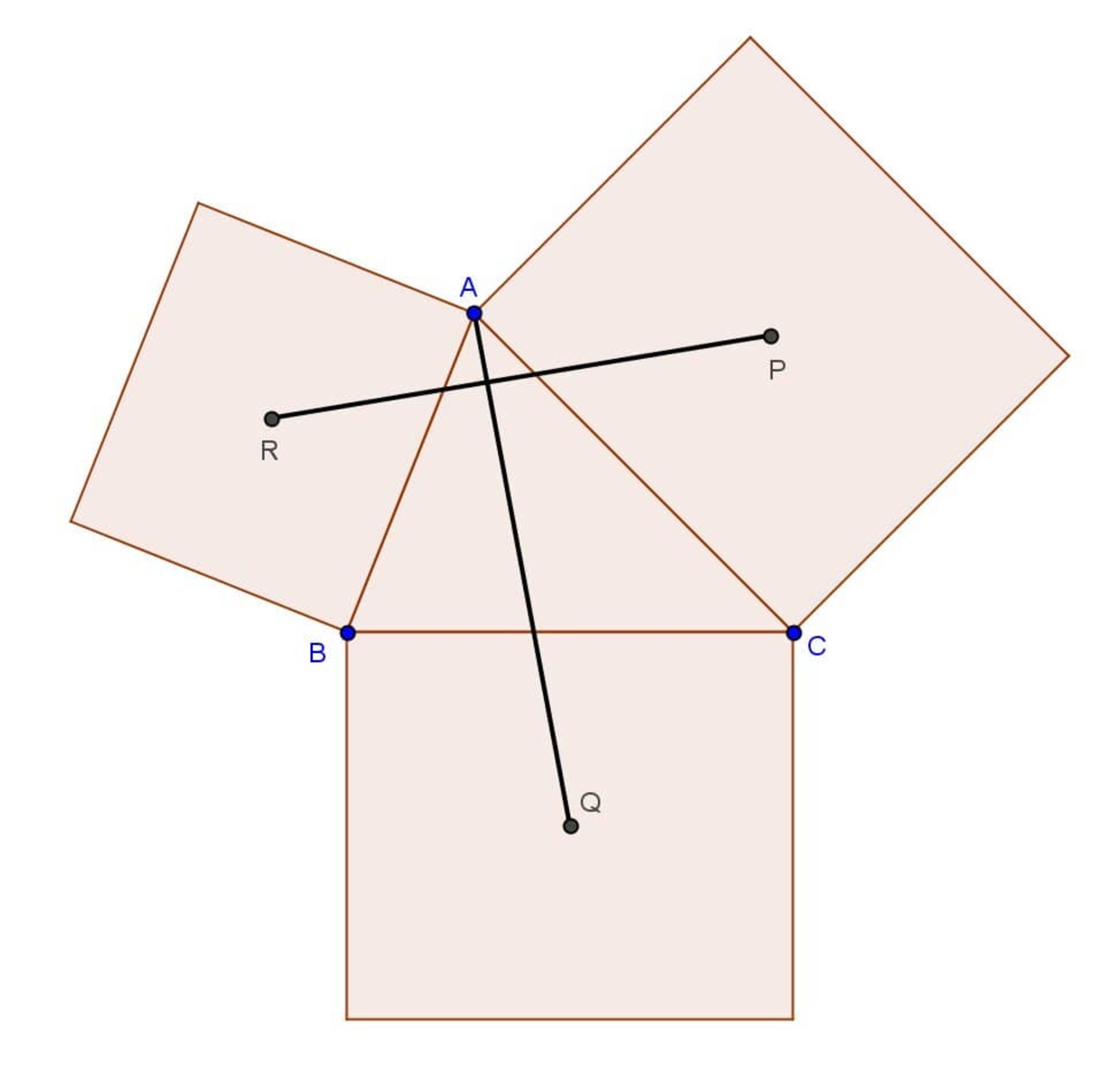
Look at the figure. it is given a scalene triangle ABC. A square are drawn in each of its sides. If points P, Q and R are the centers of the square. Prove that: 1. RP perpendicular to AQ and 2. RP = AQ.

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Here's a proof if you're familiar with complex numbers:

Let the complex numbers $a,b,c$ stand for the points on the triangle. Then $\large p=c+\frac{\sqrt{2}}{2}(a-c)e^{i\frac{-\pi}{4}}=c+\frac{\sqrt{2}}{2}(a-c)(\frac{1}{\sqrt{2}}(1-i))=c+\frac{1}{2}(a-c)(1-i)$

$\large p=\frac{1}{2}c(1+i)+\frac{1}{2}a(1-i)$

By analogy,

$\large q=\frac{1}{2}b(1+i)+\frac{1}{2}c(1-i)$

$\large r=\frac{1}{2}a(1+i)+\frac{1}{2}b(1-i)$

Giving,

$\large a-q= a-\frac{1}{2}b(1+i)-\frac{1}{2}c(1-i)$

$\large p-r= \frac{1}{2}c(1+i)+\frac{1}{2}a(1-i)-\frac{1}{2}a(1+i)-\frac{1}{2}b(1-i)$

$\large = \frac{1}{2}c(1+i)-ia-\frac{1}{2}b(1-i)$

$\large =-ia+\frac{1}{2}b(i-1)+ \frac{1}{2}c(1+i)$

$\large =-ia+\frac{1}{2}b(i-1)+ \frac{1}{2}c(i+1)$

$\large =-i(a-\frac{1}{2}b(1+i)- \frac{1}{2}c(1-i))$

$\large =e^{-i\frac{\pi}{2}}(a-q)$

QED

A L - 8 years ago

I was expecting proofs along the lines of complex numbers of vectors, which would be considered a standard exercise. There's a more basic approach, which uses similar ideas.

Hint: Let the square be labelled $ABDE$ . Consider triangles $ABQ$ and $EBC$ . Consider triangles $ARC$ and $AEC$ . Hence, we get fact 2. Show further that $EC$ makes a $45^\circ$ angle with both $AQ$ and $RP$ , which gives fact 1.

Calvin Lin Staff - 8 years ago

Thank u mr calvin for your hint. Just want to give a correction. Is it true that we should consider ARC and AEC, i think we should consider triangle ARP and AEC. Thank u. It was helping me a lot.

Falensius Nango - 8 years ago

thank u...

Falensius Nango - 8 years ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$