Geometric solution
I found a trigonometric solution to the following problem:
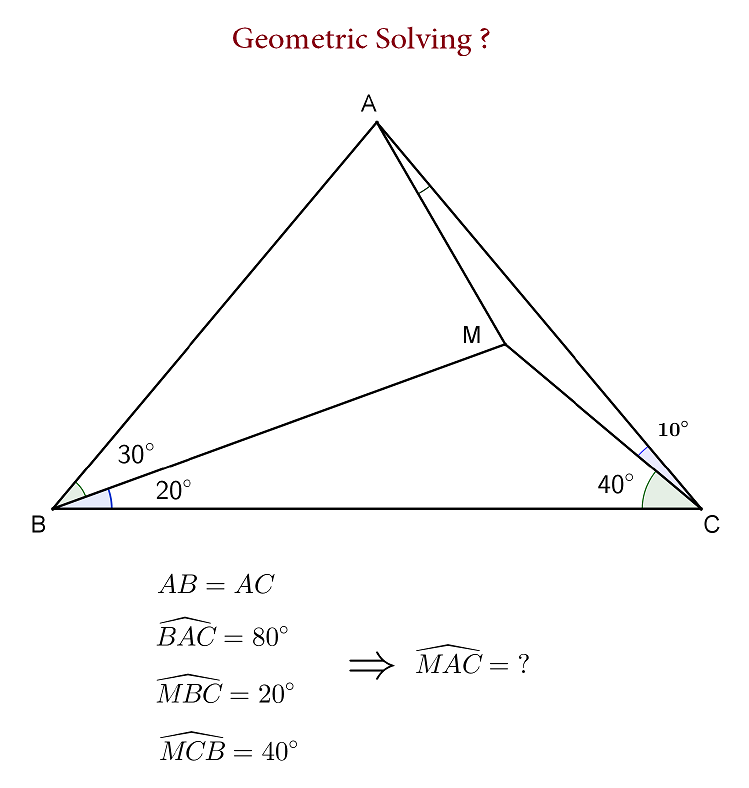 Can you find a solution without using trigonometry?
Can you find a solution without using trigonometry?
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Redefine point A to satisfy MA=MC and ∠MAC=∠MCA=10∘. So, now it suffices to prove that ∠ABM=30∘ or AB=AC. Let D be a point (below BC) such that MB=MD,∠BMD=40∘, and MD∩BC≡E. Denote I as the incenter of ΔMEC.F∈BM:ME=MF,G∈BC:FE=FG. Clearly, ΔMDA≅ΔMBC⇒∠MDA=20∘,∠MAD=40∘,∠CAD=50∘−−(1)
We have; ∠MFE=70∘ and ∠MIE=90∘+2∠MCE=110∘⇒ quad. MIEF is cyclic. Also, since ME bisects ∠IMF⇒IE=EF=GF Now, note that ΔBFG∼ΔCEI by AAS− similarity ⇒BF=CE But due to symmetry in isosceles ΔBMD,BF=ED Combining the two we get, CE=ED⇒∠MDC=30∘∴, from result (1)∠CDA=50∘=∠CAD⇒CA=CD Also, ΔMCD≅ΔMAB⟹AB=CD=AC. And, so done. Q.E.D
Log in to reply
Beautiful solution, thanks :)
Have you tried an algebraic solution to this, involving all the unknown angles?
P.S. All the methods used still fall under the banner of "trigonometry", as ultimately we are studying triangles.
Log in to reply
I used sin law several times and then a trigonometric equation comes out for the unknown MAC angle. Solving this equation gives MAC=10 degrees. But I wanted to use only basic geometric rules like parallel lines, isosceles triangles, sum of angles of a triangle. For example if we could prove AM=MC then problem is solved.
Log in to reply
You can solve it algebraically, as i said, in terms of the unknown angles, for which there are four. Fortunately, all the equations will be linear, so you will need to (hopefully) find four relations from the triangle that allow you to solve using linear algebraic methods.
To start you off, the angles around M add up to a full circle, so you can find a relation between two of the four unknown angles (as one of the angles is easily obtainable); this relation would namely be the sum.
@Kazem Sepehrinia Well, I don't have a solution without trigonometry, but we can definitely solve it quickly by applying the Sine Rule to Triangles AMC and AMB and take advantage of the fact that AB = AC along with AM = AM (the common side).....!!
Log in to reply
There are four unknown angles (as the fifth can be easily obtained), and four possible relationships involving the unknown which turn out to be all linear in the unknowns. This must mean that a linear algebraic solution can easily be obtained.
i found a solution with basic geometry and got the answer 10 ... is it correct?
Log in to reply
Yup...........the answer is 10 degrees..........Post your solution please...
You've got it right.. Please post your solution :)
please draw step by step with me... extend AB to meet AC at D.Again extend MD to reach a point E which MD=DE.So as you can see AM=AE and triangle EBM is equilateral. Take a point P in triangle MEB such that angle PBA=10.Thus,two triangles ABP & AMC are congruent.So we got that AP=AM=AE and angle MAP=80 and PB=CM. Draw a circle with radius AM.As you can see angle PAM=2*PEM=80>>>>PEM=40>>>>>BEP=PBE=20>>>>>PB=PE. PB=BE PM=PM(common)>>>>>>>>>>>>>>>>>>>>triangles MPE & BPM are congruent>>>>>>>angles EMP=PMB=30>>>>>>>>angle PAE=60(in circle) BM=Em So triangle PEA is also equilateral>>>>>EP=AM=BP=CM. after all sorry for my English.... :)
Log in to reply
Nice natural approach:)) There is a bit typo in the first line, it should be "CM" rather than "AB".
I have also a new method
I have proved it without congruence
try. this.. or **else . .. draw a perpendicular from a on bc.. and now. daw. the same figure symmetric abt.. AP then mark the point on AP where lines intersect as Q .. then.. produce. BM. till it meets AC .. and then also drop a perpendicular from M on AC name it N .repeat same... symmetrically. on othr side.. then.. use. basic geometry..(properties of isosceles triangle. and.. exterior angle theorem and. solve fr all the angles.. .. you will realise that. angle ANM is equal to angle AQM. equal to 70 degress. then use again properties of similar triangle.. n find. 2x=180 -2(70)=> x=20 this. is entirely. geometry
Log in to reply
Sorry, but the correct answer is 10 degrees.............
ABC is a triangle with angle bisector AD,BE,and CF. If angle FDE = 90 degree then find the angle BAC?
Log in to reply
120∘ ---
Log in to reply
DUDE...........you beat me to it.......I was about to answer!!! XD
How it is came? Send me the COMPLETE solution .In this way i would able to findmy mistake. Of Q1, ABC is a triangle with angle bisector AD,BE,and CF. If angle FDE = 90 degree then find the angle BAC
I have solve it
It is 10
Compas, D Scale, Triangle Scale and many more types of equipment for geometry diagram. Here ( https://www.mistersaad.com/ )Mobile app developer create Geometry application with complete Guide.
every good article. I am going through a few of these issues as well. Also, I am creating the latest trend websites you can visit my web site: https://www.adwebstudio.com/web-design-company-dubai
Thanks a lot for this Geometric solution post. Keep up the good work. I’ll be coming back lots. I am working on a web design company and we create all kind of websites you can visit our website: https://www.adwebstudio.com/web-design-company-riyadh-jeddah-saudi-arabia
take a protector.. scale compass.. draw thefig. and measure