Geometric/Algebraic Inequality
I have a geometric proof if anyone could try and prove. Keep in mind for the following:
1. Sides a,b,c form a triangle.
2. Sides (a+x),(b+y),(c+z) also form a triangle.
3. x+y+z=0.
4. Assume without loss of generality that a>b>c, and x>0.
Thanks!
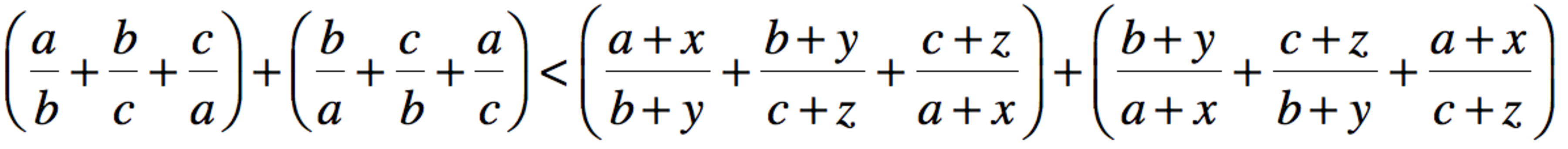
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
I don't think condition 4 is a "without loss of generality".
Log in to reply
Could you explain that? I don't really understand why not. Thanks.
Log in to reply
Say that a=11,b=10,c=9 and x=−1,y=0,z=1. How do you want to reorder the terms (IE WLOG) such that your condition 4 holds?
Log in to reply
Maybe we could let x=1 ? That satisfies the fact the x>0. I'm just trying to say that the greatest's (of sides a,b,c) corresponding x,y,z should be assumed to be positive, which would help with the proof. :D
Log in to reply
Why can we let x=1? a,b,c,x,,yz are "constants" that are given, and we cannot simply let them be what we want them to be.
However, "help with the proof" could be elaborated on better. If we can show that when a,b,c and x,y,,z are similarly ordered, then the RHS decreases, then yes we could make the assumption that a>b>c and x>y>z, which gives us x>0.