Geometry Contest!

Rules of the contest:

1.Suppose problem $i$ is posted. The one who solves the problem and posts the solution becomes able to publish the $i+1$ problem.

2.This will continue until the problem posted is not answered within $2$ hours. If the solution is not posted, the problem maker himself starts with the next problem, posting a solution of the previous one.

3.The deadline question will be declared later. Meaning, the question with which the contest ends.

4.Whosoever posts a new problem should post on slack in #general that new problem is up!

5.The new problem poster should know the solution of his posted problem.

6.If the new problem is not posted in 15 minutes of answering the previous question, ANYBODY can post a new question.

7.Marking scheme is none, This time the question setter will decide the marks, Out of 5 and the one who answers will be given that credit. The marks will be set acc. To the level of the question as in brilliant!

8.We are starting from Question 1.

Points table:

1.Prince Loomba:8 marks

2.Julian Poon:5 marks

3..Michael Fuller:4 marks

4.Ayush Rai:3 marks

EDIT: the contest has been moved

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Problem 9 [5 marks]

Let $X$ and $Y$ be points inside equilateral triangle $ABC$ . Let $Y'$ be the reflection of $Y$ in line $BC$ . Prove that

$XY+XB+XC \geq Y'A$

Sharky Kesa - 4 years, 10 months ago

We will consider the worst case. Here YYprime is max. So Y is at A or YYprime=2hA (altitude from A to BC). Now to minimise LHS, we will take X as centroid otherwise XA+XB+XC will be greater. So we have to prove that 2/3 (Ma+Mb+Mc)>2hA

Or Ma+Mb+Mc>3hA

Prince Loomba - 4 years, 10 months ago

Your first statement is unjustified, so technically, you are incorrect. You need not consider worst-case scenarios. In these questions, you must apply generally, not just in the worst-case scenario.

@Sharky Kesa – Why If we prove for worst case when LHS is minimum and RHS is max then also LHS is greater, inequality is proved. Thats a rule.

@Prince Loomba – But why is the worst-case scenario at Y? These are the sorts of questions you must answer in a proof. Otherwise, your proof is considered null as it only considers one case.

@Sharky Kesa – I am ready to reply. Because Y'A is maximum when YY' is maximum. And maximum value of Y on perpendicular to BC can be A as after A it will move out of the triangle

@Prince Loomba – I'm sorry, but this is not correct. This is still not justifying why this is true. Why is this the worst case scenario? What if Y=C (hypothetically)? This must all be answered. To define a worst-case scenario, you must describe why it is, why it can't occur anywhere else. Please, don't use wors-case scenarios in Geometry as it is very complicated.

Repost the problem 8.

Harsh Shrivastava - 4 years, 10 months ago

I am very bad at geometry so this is my concept. For minimizing XY+XB+XC we need x to be infinitely close to either points B or C and Y to be infinitely close to X. so if X is infinitely close to point B then XB + XC+ XY= XC+0.000.....0001+0.000.....0001=XC+0+0=XC or if X is infinitely close to point C then XB + XC+ XY= XB+0.000.....0001+0.000.....0001=XB+0+0=XB. As y is infintely close to x, y prime = x prime. As x is infinitely close to B or C. y prime is equal to B prime or C prime in that case. Since the triangle is equilateral XA=XB=XC so we can say XY+XB+XC can be equal to Y'A. IF you take any other case you will find that XY+XB+XC is greater than Y'A. So the equation is true

Armain Labeeb - 4 years, 10 months ago

Your reasoning is very flawed so I'm afraid you are incorrect.

I am only 13 and very bad at geometry. if there is a problem, pls ignore. also, my english is not good

Am I right till now?

Ok I will still try to prove AGAIN using scenarios.

Ok so let's first minimise XY+XB+XC. Suppose X=B=Y then XB=XY=0 OR X=C=Y then XC=XY=0. We know that AB=AC=BC=B'C. Then X'=Y'=B' or X'=Y'=C. So A is the furthest point from X and Y. I will prove that the the worst scenario of LHS is the best scenario of RHS. Ok I will let X be a tpont B (works for C too). Since X=B=Y, XB=XY=0 and XY+XB+XC=XC=BC only. Now the furthest length from A that Y can be at is at point X which is either Point B or C. YA=Y'A=BC=AB=AC=XY+XB=XC. So it is possible that XY+XB+XC=Y'A. -eq(1)

Now to prove that LHS can be greater than RHS, let's take X=centroid of triangle than XA=XB=XC and Y be at the furthest point from A which is B and C. So XY+XB+XC=3XA=3XB=3XC. and AY'=AY. Clearly 3XA is greater than YA because Y is not close to being 3 times as far from X. SO, XY + XB+XC >Y'A. -eq(ii)

Combining two equations we have

Thhats what I was saying the worst case is Y=A and X=centroid

You haven't shown why it is possible for X or Y to be placed elsewhere and satisfy. You've considered some cases, not the entire general thing.

@Sharky Kesa – So one more case will do it?

@Armain Labeeb – No you are on the wrong track. We have to prove this is the worst case i.e, LHS cant be less than this and RHS cant be greater that that

@Prince Loomba – I did didnt I?

@Sharky Kesa – Let me prove this. You understood Y=A is worst case?

@Sharky Kesa – I have proved that LHS can be greater than RHs and also that LHS can be equal to RHS and why LHs cannot be less than RHS. What more proof do you need? If I put X and Y in random points then will it be complete?

https://i.imgur.com/xmrurud.png

come to https://brilliant.org/discussions/thread/brilliant-geometry-contest-season-1/.This problem is shifted there.

Ayush G Rai - 4 years, 10 months ago

Ok I will try more cases.

See this,

IF X=Y=B or X=C=Y then the equation holds true that LHS=RHS.

IF X=Y is close to B or C the equation holds true that LHS>RHS

IF X=Y=A then the equation holds that LHS>RHS

IF X=Y is close to A then the equation holds that LHS>RHS

IF X=B or is close to B and Y=/=X and is far from B then the equation holds that LHS>RHS

IF X=B or is close to B and Y=/=X and is near B then the equation holds that LHS>RHS

IF X=C or is close to C and Y=/=X and is far from B then the equation holds that LHS>RHS

IF X=C or is close to C and Y=/=X and is near B then the equation holds that LHS>RHS.

IF X=centroid or is close to B and Y=/=X and is far from the centroid then the equation holds that LHS>RHS

IF X=centroid or is close to B and Y=/=X and is near the centroid then the equation holds that LHS>RHS

So LHS is greater than or equal to RHS

Done.

You will have to prove 'in geenral ' , not case by case coz there are infinite cases.

@Harsh Shrivastava – all types of cases are part of these cases though.

I have given you 10 cases

Problem 4 [2 points]

Suppose your house is at coordinate (1,1)

You want to visit your friend's house which is located at coordinate (-3, 5)

However, you want to first walk towards the sea to collect seashells, and then walk to your friend's house.

The coastline is described as the line $y=0$ , you can visit any point of the line to collect your seashells.

Now, what is the minimum distance you would have to walk?

Julian Poon - 4 years, 10 months ago

$2\sqrt{13}$

Reflect the point $(-3,5)$ in the $x$ axis and walk from $(1,1)$ to $(-3,-5)$ in a straight line. Using Pythagoras this is $\sqrt{6^2+4^2}=\sqrt{52}=\large \color{#20A900}{\boxed{2\sqrt{13}}}$ . Now reflect the part of the line below the $x$ axis in the $x$ axis, and this is the minimum distance

Michael Fuller - 4 years, 10 months ago

The answer is $\sqrt{52}$ or $2\sqrt{13}$

Oh boy, that means I have to post another one

My point is if you were to only go to your friends house you d have to cross the y axis. then you the minimum distance should be the just the distance from your house to your house which can be solved by pythagoras theorem. if the distance was a. then i have

a^2 = 2×4^2. because the difference between x and y coordinates of both x and y is the same which is 4.

Solving we have a=sqrt 32

The x- axis is the coastline and not y- axis.

@Ayush G Rai – Right. Its sqrt 52

Yes I also think this

Question 1[3marks]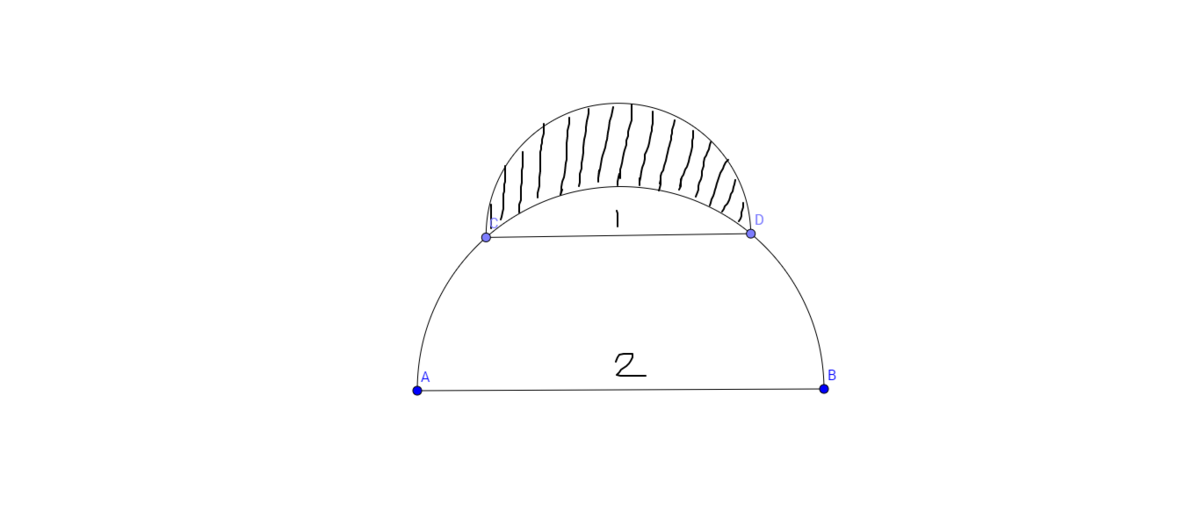 A semicircle of diameter $1$ sits at the top of a semicircle of diameter $2$ ,as shown.The shaded area inside the smaller semicircle and outside the larger semicircle is called lune.Determine the area of the lune.

It is the correct answer.

@Ayush G Rai – Thanks, I will post new soon

Question 2 (2 marks)

Find perimeter of the figure.

The above figure is a square with an equilateral triangle $AED$ "indented" into it, since all angles are $60^{\circ}$ . Therefore $AE=ED=AD=12$ , and the perimeter is $5 \times 12 = \large \color{#20A900}{\boxed{60}}$ .

Right Post next problem

Nice solution. I was thinking of a solution when you posted this. You win haha :P

@Armain Labeeb – Hehe. Posted the next problem.

Question 3 (3 marks)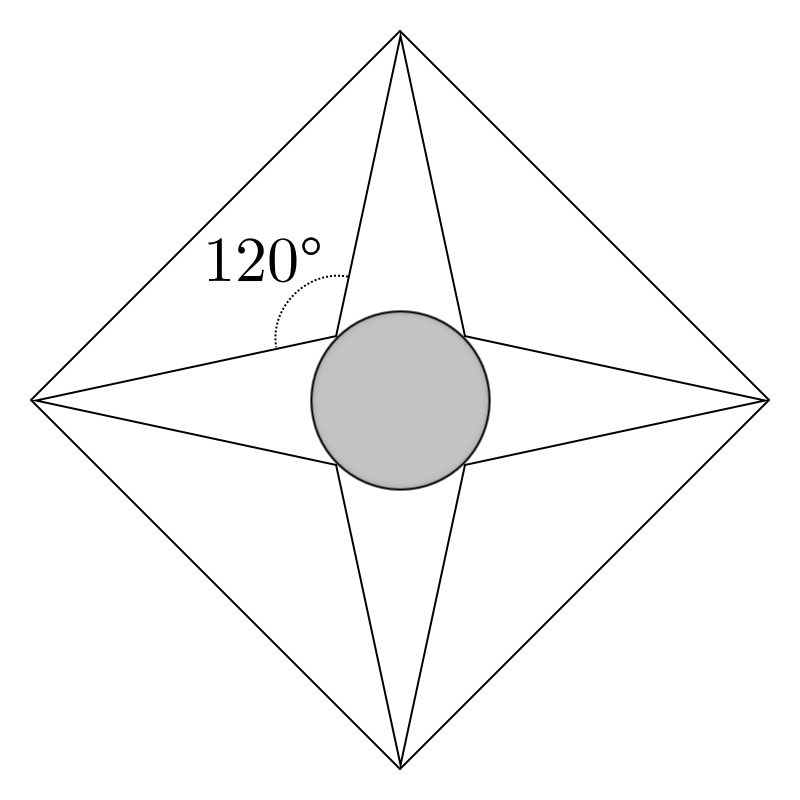 The above figure shows a medal, comprised of a square of side $1$ with a four-pointed star inscribed in it, such that the angle between the points is $120^{\circ}$ as shown.

If the area of the circle inscribed in the star is $\dfrac{a-\sqrt3}{b} \pi$ for integers $a$ and $b$ , find $ab$ .

Its 2D ?

And only of 3 marks?

Yes, the figure is 2D. My solution is not too complicated, but also harder than your 2 marker, hence I will reward 3 points for it

@Michael Fuller – Haha TIT FOR TAT

I posted 2 marks and you 3 marks comparing with me

The answer is 12.

To see why, the radius of the circle is half the length of the side minus the height of the triangle.

This gives

$r=\frac{1}{2}-\frac{1}{\sqrt{3}}$

THe area of the circle is $\pi r^2$

THis gives the area of the circle:

$\frac{2-\sqrt{3}}{6}*\pi$

Winner!

Post next

Area is $\frac{2-\sqrt3}{6}\pi$ thus , answer is $\color{#20A900}{\boxed{12}}$

Aman Rajput - 4 years, 10 months ago

Julian already got it.

Correct, but Julian answered first $:)$

Problem 5 ( $x-1$ marks)

An equilateral triangle of side $1$ has a circle inscribed in it, so that it touches all sides of the triangle at their medians. An equilateral triangle is inscribed in the circle.

The process of circle inscribing and triangle inscribing is repeated until infinity. Find the exact value of the sum of the areas of all triangles.

If the value is in the form $\dfrac{\sqrt{x}}{y}$ , find $x+y$ .

Haha x-1 marks is x used up in the question, right?

Indeed $:)$

The answer is $\frac{\sqrt{3}}{3}$ .

Each smaller triangle's area can be seen to be 1/4 of the triangle bigger than it.

For instance, the first triangle's area is $\sqrt{3}/4$ . THe second triangle would be that area divided by 4. The third triangle would be the second divided by four again and so on.

Hence, summing all the areas, the total area gives $\frac{\sqrt{3}}{3}$

Correct! $x-1$ marks for you good sir.

@Julian Poon the answer is 6 not sqrt3÷3 you have to x+y not the whole. But that doesnt matter because your solution is right.

@Armain Labeeb – Ah well...

Problem 6 [2 points]

What is the area of the largest circle possible with center at coordinate (0,0), but doesn't intersect the area bounded by $y>\frac{1}{\left|x\right|}$ ?

Simple, easy question. We wish to find the shortest distance between the Origin and this graph. But this can be easily done as follows: We have $y = \frac{1}{|x|}$ and we wish to minimise $x^2 + y^2$ (Using distance formula). Substituting $y^2 = \frac {1}{x^2}$ , we have $x^2 + \frac {1}{x^2}$ . Note that $x^2$ is non-negative, so we can apply AM-GM to get that its minimum value is $2$ . Thus, the minimum distance between the curve and the origin is $\sqrt{2}$ . Thus, the largest circle satisfying has a radius of $\sqrt{2}$ , so it has an area of $2\pi$ .

I have a short trick. The nearest point is (1,1) and (-1,1). And if circle is bigger than that, then it will be excluded. So circle covering 1,1 and center origin area is 2pi

Is the ander 2pi?

Same here, 2pi

Correct!

Post next bro

@Prince Loomba – Sorry my net was down a bit.

Problem 7 [3 points] Suppose the medians of a triangle are 5,12,13 units.Find the sides of the triangle.

26/3,2(sqrt244)/3,2(sqrt601)/3

correct!

Post next bro.

Beat me to it!!! Can we please post proofs of why it is true?

ya! sharky is right.@Prince Loomba post your solution.

@Ayush G Rai – BTW, my method is using formula $AB^2 + AC^2 = 2(AD^2 + BD^2)$ , then using simultaneous linear equations.

@Sharky Kesa – Even i used the same thing.

@Ayush G Rai – Why am I awarded points even though I didn't posted the solution to previous problem?

@Harsh Shrivastava – you didn't.really?

@Ayush G Rai – Its a direct formula. Side= $\frac {2}{3} \times \sqrt {2 ((m_{a})^2+(m_b)^{2})-{m_{c}}^2}$

@Prince Loomba – oh..thats nice

Problem 8 [3 marks]

Prove that the locus of a centre of a circle touching both another circle and a straight line which in turn do not intersect is a parabola

eg.

Let $C_1$ be the required circle and $C_2$ given circle and $L_1$ be the given line then:

$C_1$ touches $L_1$ and $C_2$ .
$C_2$ does not touch $L_1$ .

Problem looked familiar. https://brilliant.org/problems/locus-of-circles-centre/

But the proof is great.

@Prince Loomba – True, but I found this problem not too hard to show via co-ord geom. Still, my problem to post?

Try the proof without seeing. Its great really

You did a wrong thing by posting the link. You should have written your solution.

@Prince Loomba – Would've taken too long. Sorry. Also, I recognised the question (Eidetic/Photographic memory).

Its mine solution. So thats cheating.

You just copied his solution :P

@Armain Labeeb – i wrote it.How can you say that?our handwriting is same

@Ayush G Rai – Well I took his solution and your solution and compared it pixel by pixel and compared colours. It is also mesmerizing that you took the photo at the same angle and from the smae distance and under the same light and in the same notebook of his. What is even more surprising? The solutions are the same.

_<

@Armain Labeeb – Haha. Its mine. I can identify my writing

@Prince Loomba – Maybe you two are the same people from alternate universes. :P

@Sharky Kesa – maybe

@Ayush G Rai – So, do I get the points for it?

@Sharky Kesa – no

@Ayush G Rai – K, that's fine as long as problem remains.

@Sharky Kesa – He is a bad person. See he awarded marks to himself

@Armain Labeeb – One more thing see the bedsheet behind the register, Its also same

@Armain Labeeb – well,didn't you do!

@Ayush G Rai – Post the next.

See the bedsheet behind the register, its also same! How can this be possible?

@Prince Loomba – Alternate universes.

i want to take part in this where is the present question

abhishek alva - 4 years, 10 months ago

goto the comments sorting option and click New, instead of Top. Anyways, Problem 9 is most recent. No one has solved properly.

https://brilliant.org/discussions/thread/brilliant-geometry-contest-season-1/#comment-a3f5119307e92 GO HERE

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$