Geometry

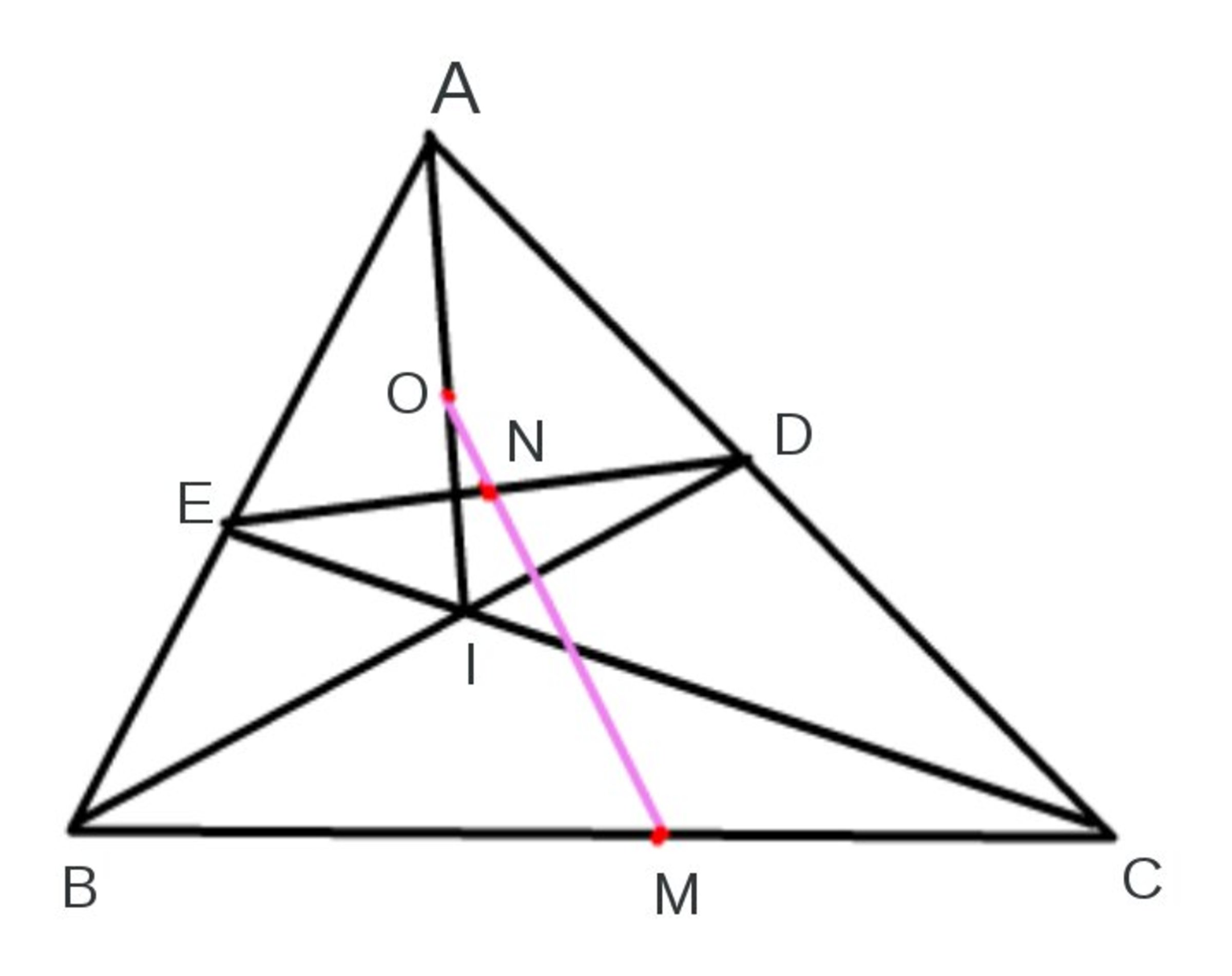
$ABC$ any triangle

Any $BD$ and $CE$ drawn such that $D$ lies on $AC$ and $E$ lies on $AB$

$DE$ drawn

$BD$ and $CE$ intersect at $I$

$AO=OI$

$EN=ND$

$BM=MC$

Prove that $M-N-O$ are collinear

#Geometry #MathProblem #Math

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

We will use normalized barycentric coordinates $A = (1,0,0)$ , $B = (0,1,0)$ , $C = (0,0,1)$ . Then $D = (p,0,1 - p)$ , $E = (q,1 - q,0)$ . Now $N$ is a midpoint of $DE$ , hence $N = \left(\frac{p + q}{2}, \frac{1 - q}{2},\frac{1 - p}{2}\right)$ Equation of line $BD$ is $pz = (1 - p)x$ and equation of line $CE$ is $(1 - q)x = qy$ Intersecting these lines we get $I = \left(\frac{pq}{p + q - pq}, \frac{p(1 - q)}{p + q - pq}, \frac{q(1 - p)}{p + q - pq}\right)$ Now $O$ is midpoint of $AI$ , hence $O = \left(\frac{p + q}{2(p + q - pq)}, \frac{p(1 - q)}{2(p + q - pq)}, \frac{q(1 - p)}{2(p + q - pq)}\right)$ And $M$ is midpoint of $BC$ , so trivially $M = \left(0, \frac{1}{2}, \frac{1}{2}\right)$ Now note that $\begin{vmatrix} \frac{p + q}{2}& \frac{1 - q}{2}&\frac{1 - p}{2} \\ \frac{p + q}{2(p + q - pq)}& \frac{p(1 - q)}{2(p + q - pq)}& \frac{q(1 - p)}{2(p + q - pq)} \\ 0& 1/2& 1/2 \end{vmatrix} = 0$ Hence $M,N,O$ are collinear.

Jan J. - 7 years, 9 months ago

I'm not sure I understand your last step. Are you taking the determinant of a matrix? I'm assuming that's what you're doing. How does that tell you that the three points are co-linear?

Sotiri Komissopoulos - 7 years, 9 months ago

The main idea is: If the area of a triangle is 0, then the vertices lie on a straight line.

Note that once you found the coordinates of the points, you could go about finding the line that these three points are on. However, unless the ratios are immediate, this often requires a bunch more algebra. Showing that the area is 0 could be more straightforward.

Barycentric coordinates merely make the algebra much easier / nicer. A coordinate geometry approach would work similarly, though with much uglier values.

Calvin Lin Staff - 7 years, 9 months ago

See here http://zacharyabel.com/papers/Barycentric_A07.pdf page 5.

Jan J. - 7 years, 9 months ago

This is the Newton-Gauss line of a complete quadrilateral.

Jon Haussmann - 7 years, 9 months ago

Why did every comment gets vote down?

Zi Song Yeoh - 7 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$