Geometry question

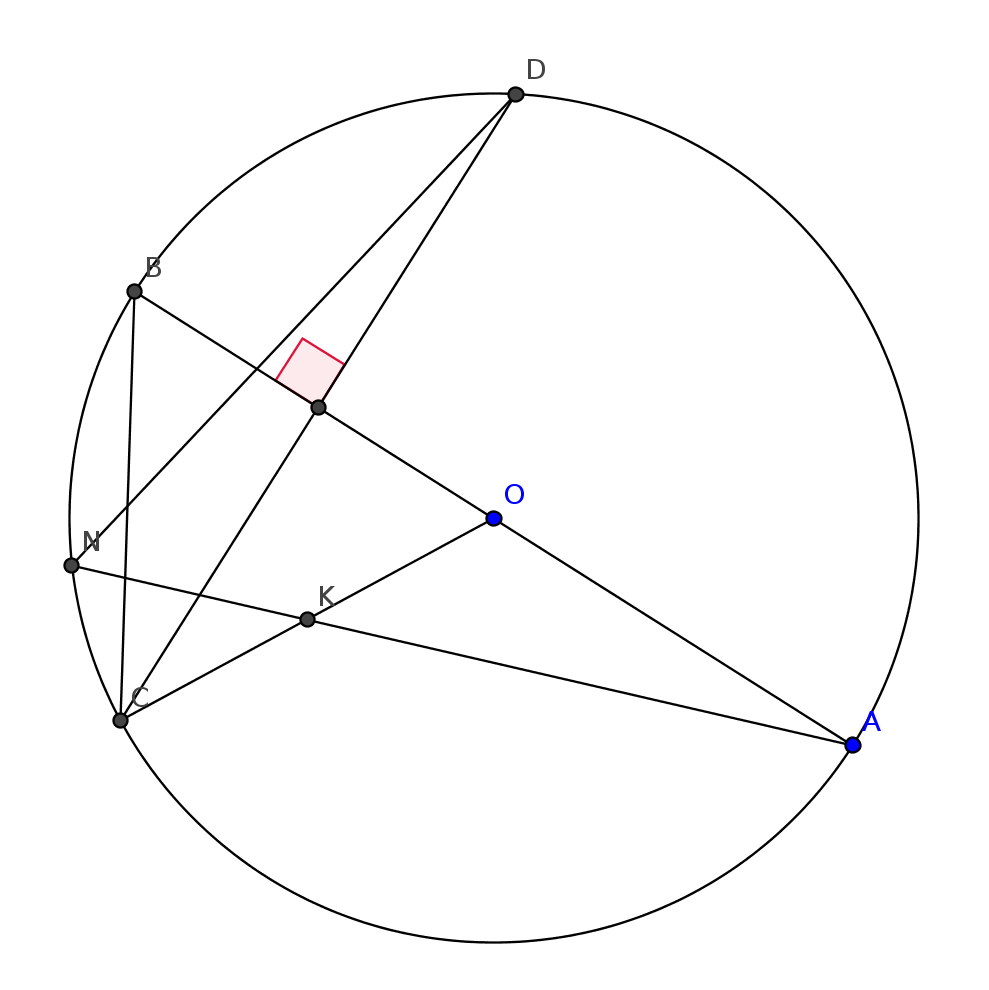
Pure geometry question

$CD$ is a chord of circle with centre $O$ .

$AB$ diameter bisecting it.

$OC$ drawn and its midpt $K$

$AK$ drawn intersecting circle at $N$

Prove that $ND$ bisects $BC$

#Geometry #Circle

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

This problem is based around this property for similar triangles: Corresponding elements in similar triangles are also "similar". This will be disguised in the following proof(more like a sketch actually):

Denote $DN\cap BC=X$

First note that $\triangle COA\sim \triangle CBD$ . By properties of circles: $\angle CDX=\angle CAK,\angle BDX=\angle OAK$ , using this we can prove $\triangle CDX\sim \triangle CAK, \triangle XDB\sim \triangle KAO$ , which gives: $\frac {CX}{CK}=\frac {CD}{CA}=\frac {BD}{OA}=\frac {BX}{OK}$ $\Rightarrow \frac {CX}{BX}=\frac {CK}{OK}=1$ $\Rightarrow CX=BX$ . Q.E.D

Xuming Liang - 7 years, 4 months ago

Thank you very much. very nice solution

Megh Parikh - 7 years, 4 months ago

(y) Nice

Rohan Chandra - 7 years, 4 months ago

Here goes my solution : Denote $\{M\} = BC \cap NK$ then we have $NCKM$ is concyclic (since $\angle KNM = \angle OBC = \angle KCM$ : I skipped a few details here, you can verify them if you will). Using the angle chasing technique, one has $\angle NKM = \angle NCM= \angle NAB \implies KM || AB$ . Now, consider the triangle $OBC$ with $KM || OB$ and $K$ is the midpoint of OC, these lead to the fact that $M$ being the midpoint of $BC$ as expected.

Viet Hoang - 7 years, 4 months ago

Elegant solution

Megh Parikh - 7 years, 4 months ago

I will provide another solution just for fun. This one I'll use something called Harmonic division, for those that are unfamiliar just google, there's a lot of papers written on this wonderful topic. Here is the 2nd proof:

Keeping $DN\cap BC=X$ , we denote $AK\cap BC=M$ .

If we want to prove $X$ is the midpoint of $BC$ , we just need $KX\parallel BO$ . Since $O$ is the midpoint of $AB$ , we now just need to prove $K(X,O;B,A)$ is a harmonic pencil $\iff$ so is $K(X,C;B,M)$ $\iff$ so is $N(X,C;B,M)$ $\iff$ $ACBD$ is a harmonic quadrilateral which is true since $BD*CA=DA*BC$ . Q.E.D

Xuming Liang - 7 years, 4 months ago

I won't explain the notations here, since it's pretty "universal" in projective geometry. Again, I encourage those that have never heard of Harmonic divisions to read about it.

Although the words "projective geometry" might sound intimidating to some of you, in terms of just harmonic division, I think we can keep everything Euclidean by just knowing the fact that cross-ratios are possible due to the ratios of trig angles etc. I know these make no sense but you will know what I mean once you read about it....

Xuming Liang - 7 years, 4 months ago

Thanks! :)

Happy Melodies - 7 years, 4 months ago

These are cross ratios right? To my knowledge, I think the way you do it is wrong? Because you stated $K(X,O;B,A)$ is a harmonic pencil, but they are not concyclic or collinear, can you do that? The part from $K(X,C;B.M)$ to the $ACBD$ as a harmonic quad is correct, but then when you project the line $XCBM$ , to the line $OBA$ , through point $K$ , you did not project $X$ . Cheers!

Yong See Foo - 7 years, 4 months ago

Ok, I think I see the confusion here. Well, $KX$ is considered to intersect $AB$ at the point at infinity on $AB$ , which is something new introduced in projective geometry. Despite that though, it can be checked that the cross-ratio(trig ratio) isn't affect when you have parallel lines.

Xuming Liang - 7 years, 4 months ago

@Xuming Liang – Alright I remember now because given two points, if the midpoint divides the segment internally, the point at infinity on that line divides it externally with the same ratio, 1. So in $K(X,O;B,A)$ , you actually meant $K(KX\cap AB,O;B,A)$ , where $KX\cap AB$ is actually point at infinity, and therefore the two lines are parallel. Thanks for that!

Yong See Foo - 7 years, 4 months ago

Bonus point to proving $AN$ trisects $BC$ , and another bonus point to proving $DN$ trisects $BO$ !

Yong See Foo - 7 years, 4 months ago

Both are trivial using Menelaus' theorem.

Xuming Liang - 7 years, 4 months ago

Yes menneeaus will prove it

Megh Parikh - 7 years, 4 months ago

Well using your notation I just play around with the harmonic conjugates $(X,C)$ and $(B,M)$ , so it's pretty much the same thing with Menelaus'.

Yong See Foo - 7 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$