[Geometry] Not Samuraiwarm's Theorem

Note: If you have seen this theorem before, please tell me.

Also if you have a proof, feel free to post it. I'm working on it too!

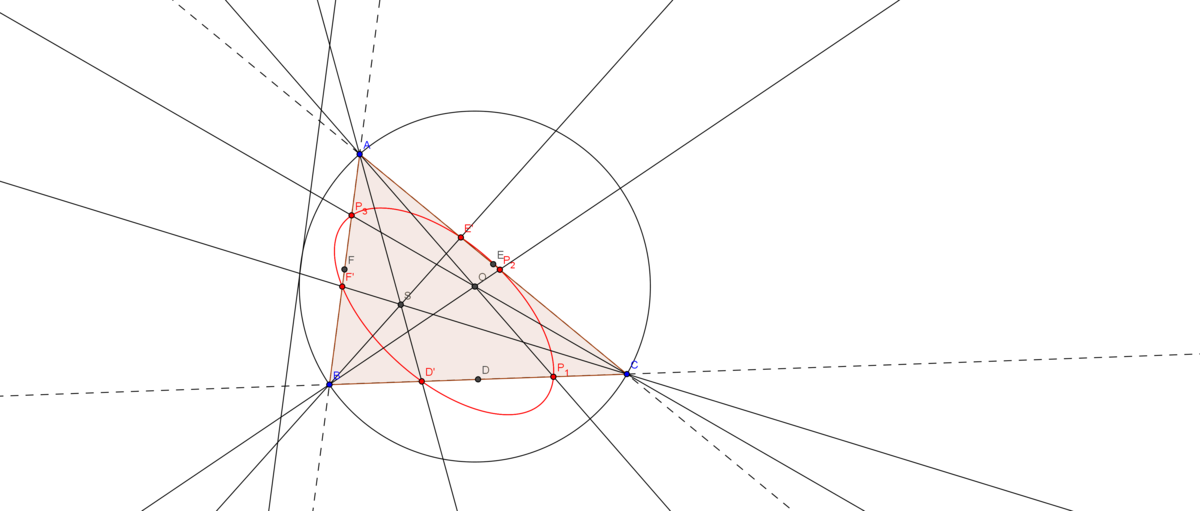
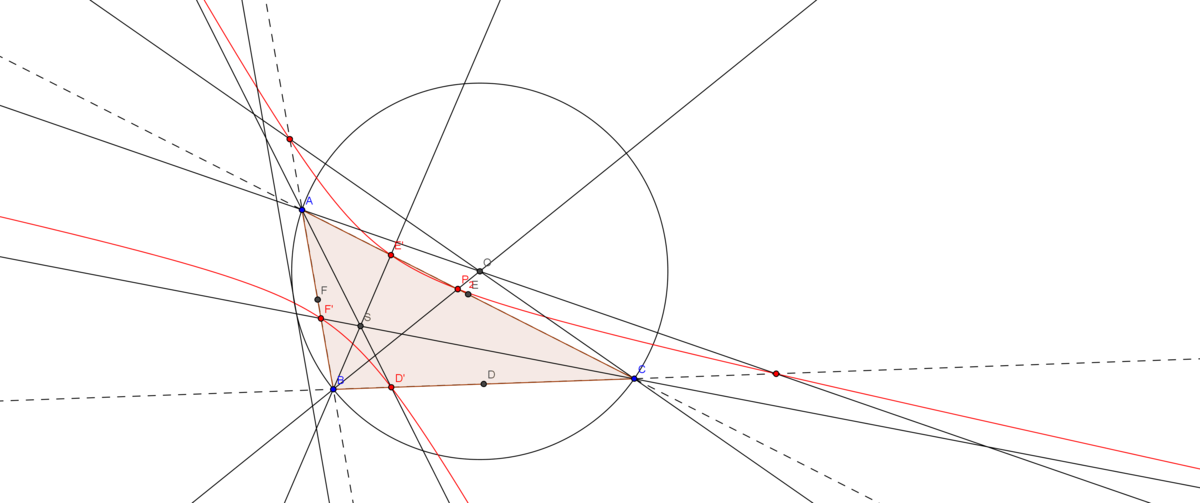
With nine-point circle

The small black circle is nine-point circle, and the red conic is what my theorem says.

Construct a triangle $ABC$ (not necessary acute), midpoint of sides $\overline{BC},\overline{CA},\overline{AB}$ called $D,E,F$ respectively, and symmedians of a triangle $ABC$ called $\overline{AD'},\overline{AE'},\overline{AF'}$ $\overline{BC},\overline{CA},\overline{AB}$ called $D,E,F$ respectively. Construct a line from $A,B,C$ , pass through circumcenter $O$ , and intersect $\overline{BC},\overline{CA},\overline{AB}$ at point $P_{1},P_{2},P_{3}$ respectively.

Theorem: 6 points, $D,E,F,P_{1},P_{2},P_{3}$ lie on the same conic.

Details: 3 symmedians of a triangle are isogonal conjugate of 3 medians of a triangle.

Details: The isogonal conjugate $X^{-1}$ of an object $X$ in a triangle $ABC$ is constructed by reflecting $\overline{AX},\overline{BX},\overline{CX}$ about the angle bisectors of $A,B,C$ .

Idea: I got this idea from a nine-point circle, where the feet of altitudes, midpoints, and the midpoints between vertices and orthocenter all lie on the same circle. I also think that the isogonal conjugates are also the same.

(Orthocenter and circumcenter are isogonal conjugate to each other. Also centroid and symmedian point are isogonal conjugate to each other.)

Side notes: If you appear to see 3 other points (the similar to the midpoint of each 3 vertices and orthocenter), please tell me too.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Well, this result is actuallyu true for any two points. In other words, any two cevian triangles of $ABC$ are conconic. You can prove this using crossratio.

Xuming Liang - 5 years, 11 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$