Got stuck at a point -2

While working with algebra, I got a very interesting equation to solve which is as follows

\[a^y=y\] \[\Rightarrow a^{a^{y}}=y\] You may continue like this and you will get \[\boxed{\red{a^{a^{a^{a^{a...}}}}=y}}\] Where $a$ is known, $a∈(0,e^{\frac{1}{e}}]$, can you solve for $y$ such that $y∈(0,e]$?

Any solution will be appreciated

#Algebra

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Chew-Seong Cheong, @Elijah L, @Yajat Shamji, @Mahdi Raza, @Kumudesh Ghosh, @Alak Bhattacharya, @Vinayak Srivastava, @Aryan Sanghi, @Jeff Giff, @Marvin Kalngan

Zakir Husain - 1 year ago

This property or in fact this question is known as tetration.

Interestingly if we let

$a^{a^{a^{a^{a^{}}}}} = 2$ $a^2 = 2 \implies a = \sqrt{2}$

And again

$b^{b^{b^{b^{b^{}}}}} = 4$ $b^4 = 4 \implies b = \sqrt{2}$

Now, since $a=b$ , $\implies a^{a^{a^{a^{a^{}}}}} = b^{b^{b^{b^{b^{}}}}} \implies 2=4$ ?

Does this mean $2 = 4$ ?

Mahdi Raza - 1 year ago

Aren't those two two different equations. So, you can't equate both of them, ain't it?

Aryan Sanghi - 1 year ago

Rethink, i have edited my comment a bit

Mahdi Raza - 1 year ago

@Zakir Husain

Mahdi Raza - 1 year ago

well all values of $a$ where $a∈(1,e^\frac{1}{e})$ follow this behaviour

Zakir Husain - 1 year ago

Yes

Mahdi Raza - 1 year ago

@Mahdi Raza - It is also a math failure, a potential Math also fails! -3. Well, what could be it's explanation?

Zakir Husain - 1 year ago

I remember seeing this question somewhere. The answer said that it is limited for some values of $a$ or $b$ , but I don't remember much.

Vinayak Srivastava - 1 year ago

This might help :)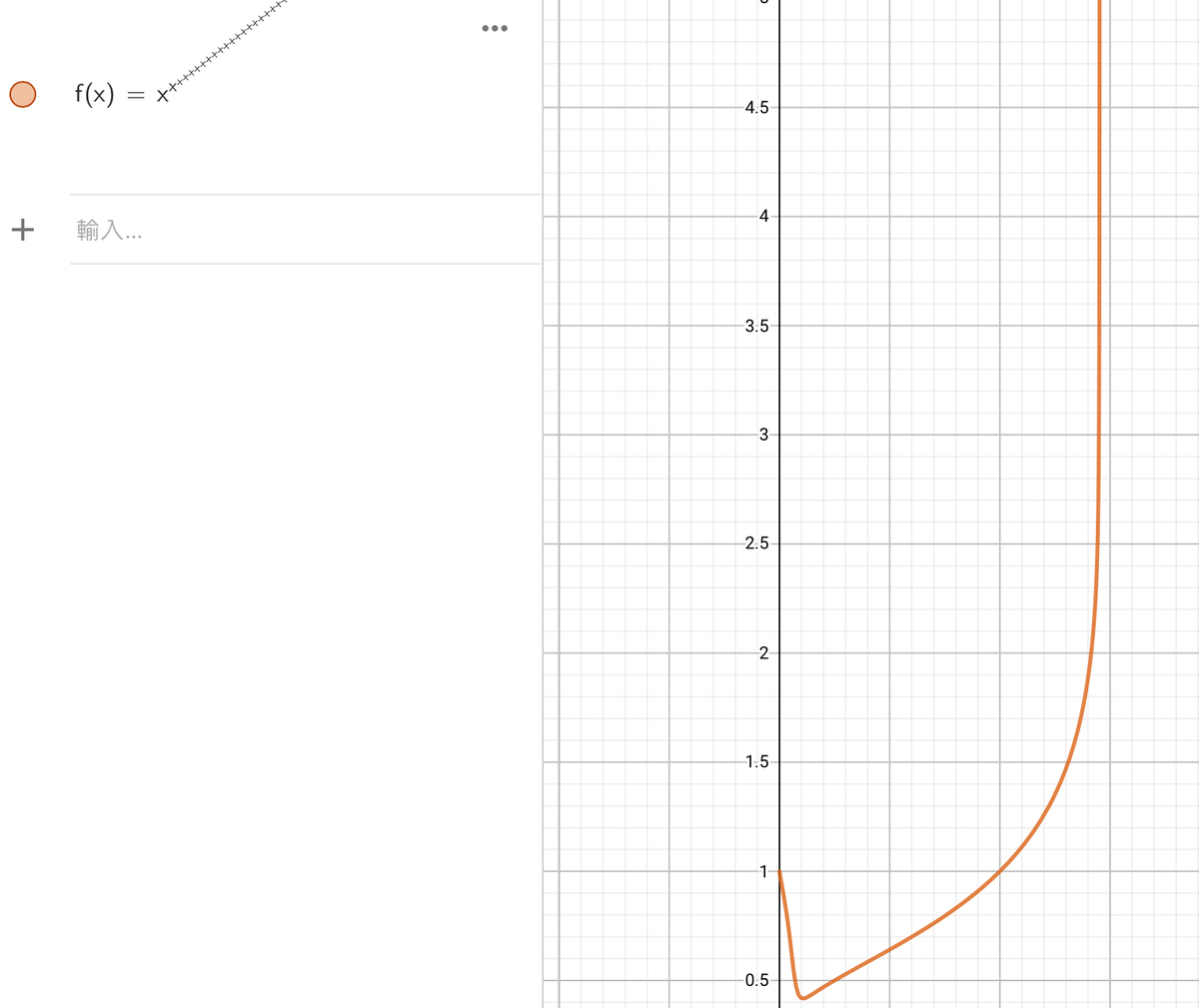 The number of x’s are finite, yet the graph starts to approach a straight line already.

Jeff Giff - 1 year ago

The straight line at the end is $x = e^{\frac{1}{e}} \approx 1.444667861009766$

Mahdi Raza - 1 year ago

@Mahdi Raza – Oh! That is interesting :)

Jeff Giff - 1 year ago

@Jeff Giff, For infinite $x$ you should graph $y=x^y$ instead of this poor approximation, because this will give you the exact graph.

Zakir Husain - 1 year ago

@Zakir Husain – Oh, I never thought of that! Silly me :)

Jeff Giff - 1 year ago

@Jeff Giff, how you put this image in the comment?

Zakir Husain - 1 year ago

@Zakir Husain – First try posting the image in a question. Then copy the link form. Finally paste it onto the comment :)

Jeff Giff - 1 year ago

@Zakir Husain – What i do is go to a previous solution, insert media, copy the location code, and paste it in the comments. It is tedious i know

Mahdi Raza - 1 year ago

@Jeff Giff, see the graph below: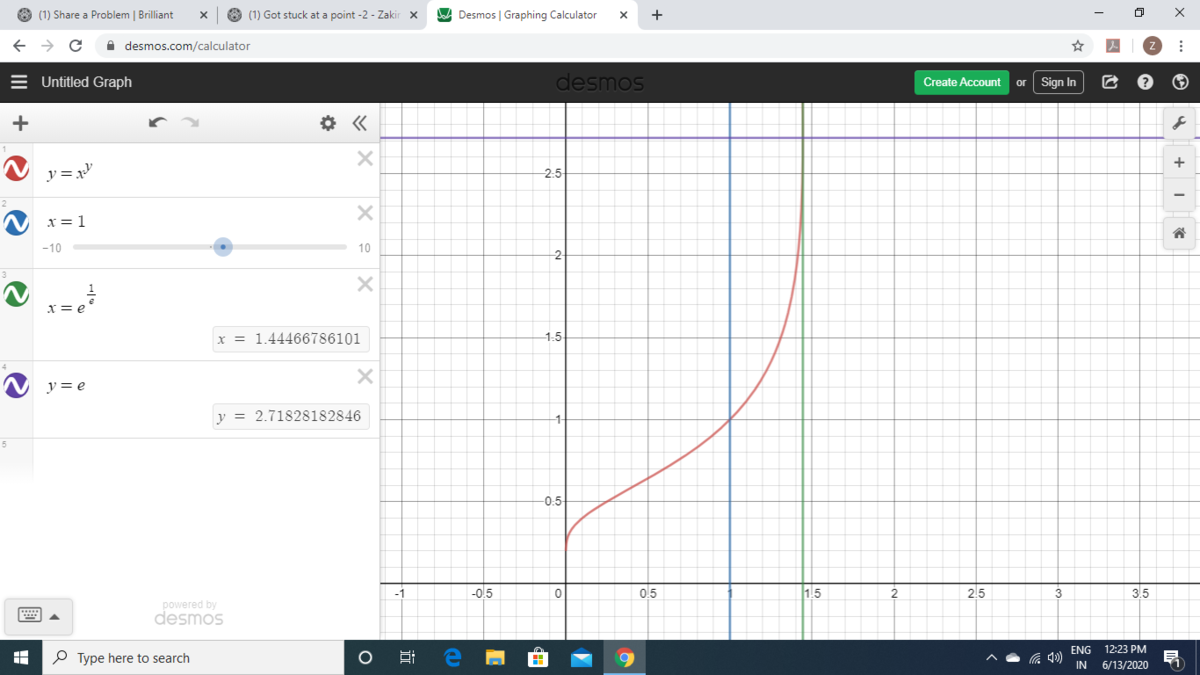

I only want a formula which relates all the $x$ and $y$ of the points of $x^y=y$ in the rectangle formed by the $x-axis,y-axis,y=e,x=e^\frac{1}{e}$ . As I said in my comment

Zakir Husain - 1 year ago

@Zakir Husain – Oh. I’ll try to help:)

Jeff Giff - 1 year ago

@Zakir Husain – Maybe it’s related to $[(x+a)^n+b]\times c$

Jeff Giff - 1 year ago

@Mahdi Raza- Explanation to the contradiction

Let $x=y^{y^{y^{.^{.^{.}}}}} \Rightarrow x=y^x$ assuming $x ≠ 0$ $y=x^\frac{1}{x}$

Now the maxima of $x^\frac{1}{x}$ is $e^\frac{1}{e}$ and for any $x | x \in (e,∞)$ , $y \in (1,e^\frac{1}{e})$ .

And for any $x | x \in (1,e)$ , $y \in (1,e^\frac{1}{e})$

So for any two variables $x_1$ and $x_2$ $| x_1\in (1,∞),x_2 \in (1,∞)$ and $x_1^\frac{1}{x_1}=x_2^\frac{1}{x_2} \nRightarrow x_1=x_2$

And in your case, applying above statement $a=2^\frac{1}{2}$ and $b=4^\frac{1}{4} \Rightarrow a=b \nRightarrow 2=4$

Zakir Husain - 1 year ago

If you haven't read the note above and the comment above yet, then kindly read them first.

@Chew-Seong Cheong, @Justin Travers , @jordi curto , @Yajat Shamji , @Mahdi Raza , @Kumudesh Ghosh , @Alak Bhattacharya , @Vinayak Srivastava , @Aryan Sanghi , @Jeff Giff , @Marvin Kalngan .

Now a new problem arises, if $x_1^\frac{1}{x_1}=x_2^\frac{1}{x_2}; x_1≠x_2$ then what is the relation between $x_1$ and $x_2$ $?$

Zakir Husain - 1 year ago

@Zakir Husain – This might help :)

Jeff Giff - 1 year ago

@Zakir Husain – $x_1,x_2$ are the $x$ values of the intersection between $x^{\frac 1x}$ and $y=x_1^{\frac {1}{x_1}}$ .

Jeff Giff - 1 year ago

@Jeff Giff – The graphs are intersecting at $(1,1)$ , that is when $x_1=1,x_2=1$ , in that case $x_1=x_2$ . I'm talking about the case
When $x_1^\frac{1}{x_1}=x^\frac{1}{x_2}$ but $x_1 \neq x_2$ . For example when $x_1 = 4; x_2=2$ ; then $2^\frac{1}{2}=\sqrt{2}=4^\frac{1}{4}$ but $2 \neq 4$

Zakir Husain - 1 year ago

@Zakir Husain – But the graphs in the pic aren’t the ones that I mentioned:)

Jeff Giff - 1 year ago

@Zakir Husain – I just meant to say that the graphs in the picture are symmetrical along $x=y.$

Jeff Giff - 1 year ago

@Zakir Husain – Also, $x_1$ is on the interval $[0,e)$ while $x_2$ is on the interval $(e,\infty]$ for $x_1\neq x_2$ :)

Jeff Giff - 1 year ago

@Zakir Husain – e.g. the graphs intersect at $(2,\sqrt2)$ & $(4,\sqrt2)$ so $2^{\frac12}=4^{\frac14}=\sqrt2.$

Jeff Giff - 1 year ago

@Zakir Husain – Two diferents values has same image :

other ejemple : f(x) = x^2

x= -2 and x= 2 => f(x) = 4

Relation is f inverse f(x) = $\sqrt{x}$

for x= 4 => f(x) = + 2 and -2

jordi curto - 1 year ago

@Jeff Giff- See here, I have already written that

Zakir Husain - 1 year ago

Solution will exist only when $a \in (0, 1)$ . Now, you can draw graphs for y = $a^x$ and y = x and find the solution.

Aryan Sanghi - 1 year ago

solution exists if $a∈(0,e^{\frac{1}{e}})$ , I recalculated it just now

Zakir Husain - 1 year ago

Anything wrong in this graph?

Vinayak Srivastava - 1 year ago

@Vinayak Srivastava - Nothing is wrong with the graph but, it is only for the case $a=1.4$ I want a general formula for the solution for any $a∈(0,e^\frac{1}{e})$

Zakir Husain - 1 year ago

@Aryan Sanghi- I am searching for a formula which gives value of $y$ for every value of $a$ where $a∈(0,e^\frac{1}{e})$

Zakir Husain - 1 year ago

$a \in (\frac{1}{e^e}, e^{\frac{1}{e}})$

Mahdi Raza - 1 year ago

Well the $e^\frac{1}{e}$ comes by taking the maxima of the function $x^{1/x}$ , but the minima is not $1/e^e$ . If you know calculus and wanted proof for the given argument, then please comment.

Zakir Husain - 1 year ago

@Zakir Husain – Sorry I haven't learned calculus

Mahdi Raza - 1 year ago

@Zakir Husain – Yes, you are right. I got same value as yours.

Aryan Sanghi - 1 year ago

@Chew-Seong Cheong, @Justin Travers, @jordi curto, @Yajat Shamji, @Mahdi Raza, @Kumudesh Ghosh, @Alak Bhattacharya, @Vinayak Srivastava, @Aryan Sanghi, @Jeff Giff, @Marvin Kalngan. For every $a∈(1,e^\frac{1}{e})$ there exists $2$ solutions for each $a$ , one of them will be $y$ such that $y∈(1,e)$ . I'm only considering that as solution for $1<a<e^\frac{1}{e}$ , for $0<a<1$ there is only one solution for each $a$ . Can anyone find any formula for these solutions where ( $\red{0<y<e}$ ). I have also edited the note a bit, because I don't need $y>e$

Zakir Husain - 1 year ago

Why mention me? @Zakir Husain. I cannot do this stuff - please remove my mentions...

A Former Brilliant Member - 1 year ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$