Got stuck at a point -3
While solving the four points on a square Bonus problem I was stuck at a last point (if someone solves this, then I can make a set of steps as an answer to the problem) please try to help.
Consider the following diagram () :
Let a process on a point that is on semicircle be defined as follows :
Join and
Extend till it intersects the semicircle at a point B
Join and extend
Draw the angular bisector of and let it intersect extended at point
Let be called as the output of the process
An illustration of process on a point on the semicircle ( line is the angular bisector) :
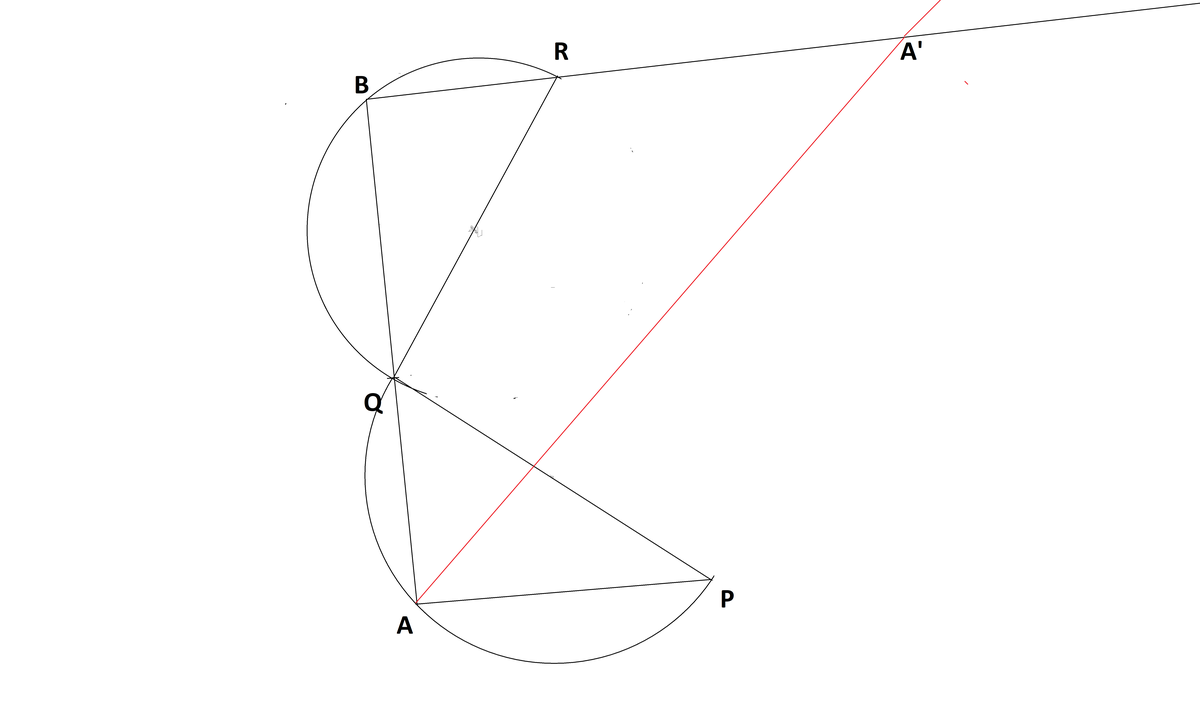
Now imagine that you does this process on every point of the semicircle and marks each and every output, what will be the shape made by those outputs? (A circle, A parabola, A square...)
Note:
Any point on the diameter is not counted as a point on the semicircle
If anyone gives the answer with a proof, I will immediately write a solution to the four point in square problem as I am just one solution far to the problem (that is this problem)
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Have a look at this, it might help :)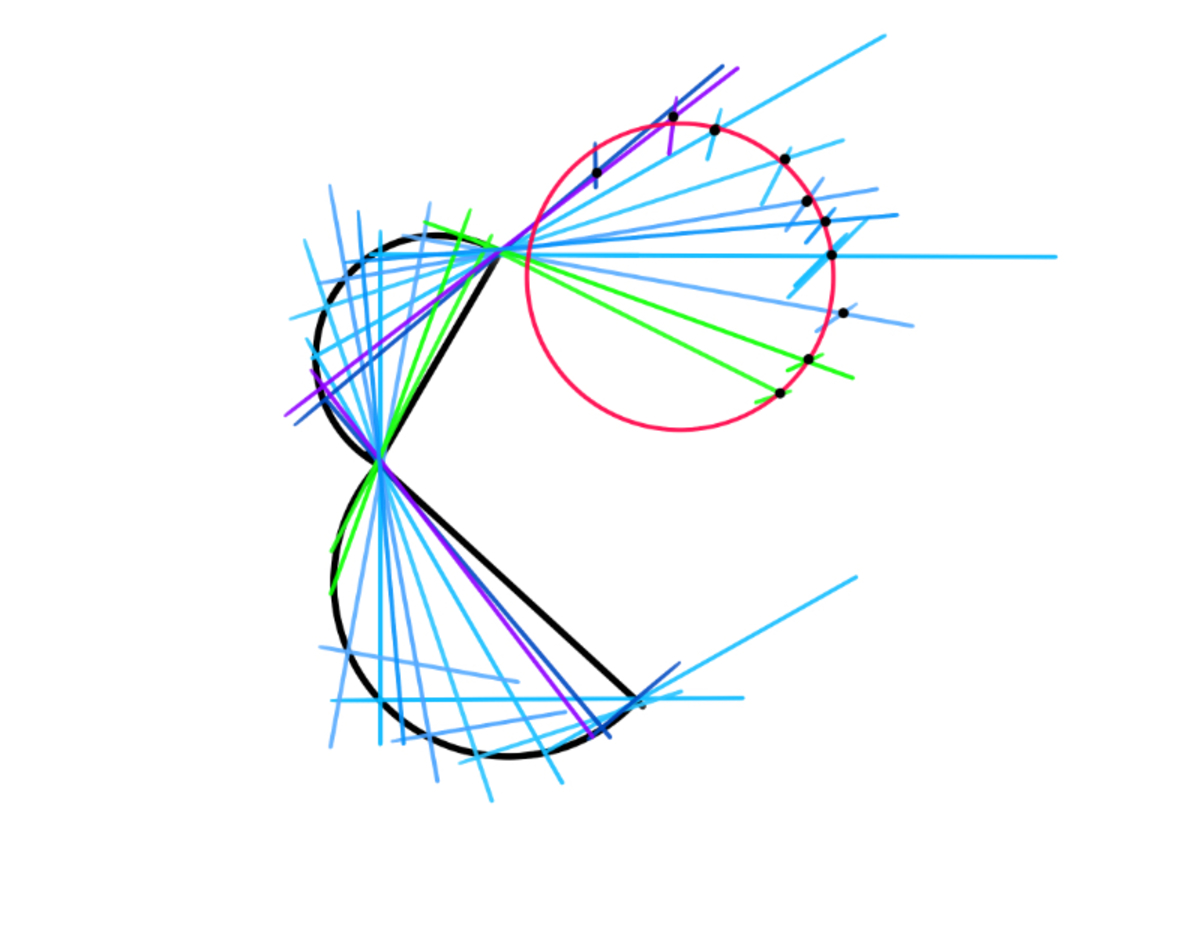
Log in to reply
Wow,how do you make it.. @Jeff Giff
Log in to reply
Sketchbook, iPad. Designed for art, but works well in these situations :)
I had also tried to make this and i also got an approximated circle, but I need a proof for that.
Log in to reply
Yes,math requires proof.I am also trying to prove.
Are QR and QP perpendicular to each other ?? Please reply @Zakir Husain
Log in to reply
No they are at an arbitrary angle
Log in to reply
Oooooooo ,
Hint: Complete the semicircles. Call the midpoint of arc PQ(the one that the angle bisector will pass through) M, and the two completed circle intersect at another point Q′. You can try to prove that R,A′,Q′,M are concyclic. (Since R,Q′,M are fixed points, this leads to the locus of A′ being a circle. A simple angle chasing will prove this. Actually, this is just a special case of Miquel's theorem, or Pivot theorem, so the proof is the same.)
Log in to reply
Hope this hint helps, and I'm looking forward to see your solution to the four point in square problem !
Log in to reply
Yes,it helps.....
I have only 1 doubt, what is the angle between seg QP and seg QR, I know it has to be greater than 0 degrees and lesser than 180 degrees, otherwise getting point B is not possible on the other semicircle, unless the point A coincides with the endpoints of the diameter or is on the diameter, which you have restricted from doing so. Also not greater than 180, because the semicircles would overlap then which I assume is not allowed.
Log in to reply
0<∠PQR<π
Log in to reply
Yes that is what I meant, thank you! I will work on the proof now and see if I can do it.👍
@Jeff Giff, @Mahdi Raza, @Vinayak Srivastava, @Kumudesh Ghosh, @Aryan Sanghi, @Marvin Kalngan, @Yajat Shamji, @Alak Bhattacharya Try to help
Log in to reply
@Kriti Kamal
This one appeared in Terence Tao (yes he!!) 's book in late 90's.