Got stuck at a point -1

While I was spending time on geometry and triangle congruence triangles a question came in my mind which I wasn't able to solve, it can be described as follows:

In the given figure $O$ is the center of the circle.

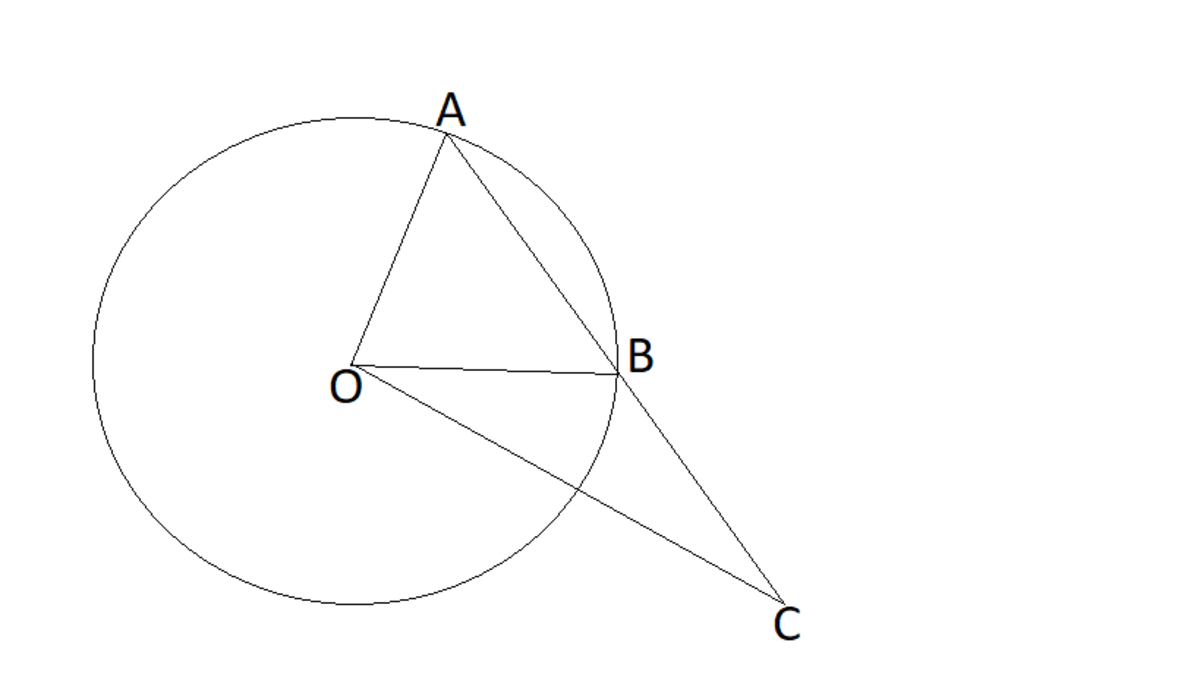
If you only knows measure of $\overline{OA},\overline{OB}, \overline{OC}$ and $\angle ACO$ then can you find measure of $\angle AOB$ ?

Any answer will be worthy and will be appreciate, so please try once!

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I will try, although I don't know much of geometry(circles and all that).

However, I think $OA$ and $OB$ are the same (radii), so only one needs to be specified.

Vinayak Srivastava - 1 year ago

Yeah, That's right

Zakir Husain - 1 year ago

I tried it, but could not do it with the geometry I am taught till now. I think it really requires higher class geometry like the solutions of Aryan Sanghi and Jeff Giif.

Vinayak Srivastava - 1 year ago

You can do it using Sine rule

$\frac{OB}{sin C}$ = $\frac{OC}{sin OBC}$

As we know, OB, Angle C and OC, we can find angle OBC

With this, we can find angle ABO with linear pair

Now, angle A is equal to Angle ABO as OA = OB

So, we can apply sum of anglea of triangles is 180° in triangle AOB to get angle AOB

Aryan Sanghi - 1 year ago

Thanks for your solution

Zakir Husain - 1 year ago

Yes, I suppose you can! Given $\frac{sinA}{a}$ = $\frac{sinB}{b}$ , you can substitute values of angle ACO and side OA, so
$\frac{sin(angleACO)}{sideOA}=\frac{sin(angleOAC)}{sideOC}.$
Since OA & OB are the radii of a same circle, triangleOAB is an isosceles triangle, so angle AOB =
$180^\circ - 2\times \angle OAC.$

Jeff Giff - 1 year ago

Thanks for your efforts

Zakir Husain - 1 year ago

$\angle OAB^{\circ} = \angle OBA^{\circ}$

In $\triangle AOC$ : $\dfrac{AO}{\sin{(ACO^{\circ})}} = \dfrac{OC}{\sin{(\angle OAC^{\circ})}} \implies OAC^{\circ} = \sin^{-1} {\bigg(\dfrac{OC}{AO \times {\sin{(ACO^{\circ})}}}\bigg) \cdot }$

$\begin{aligned} \angle BOA^{\circ} &= 180^{\circ} - 2 (\angle OAC^{\circ}) \end{aligned}$

Mahdi Raza - 1 year ago

@Zakir Husain, this answer is just a modification from @Jeff Giff's problem. I don't know which of these inspired the other, but both are nice!

Mahdi Raza - 1 year ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$