Graph Isomorphism

The graph isomorphism problem has a long history in the fields of computer science, mathematics and chemistry. Graph isomorphism is very important due to its practical applications and its unique complexity theoretic status . Informally, graph isomorphism is to check if two graphs that look different are actually the same. More formally, given two graphs does there exist a 1-to-1 mapping of vertices in one graph onto the vertices of other such that edges and non-edges are preserved?. Example of two isomorphic graphs is given below

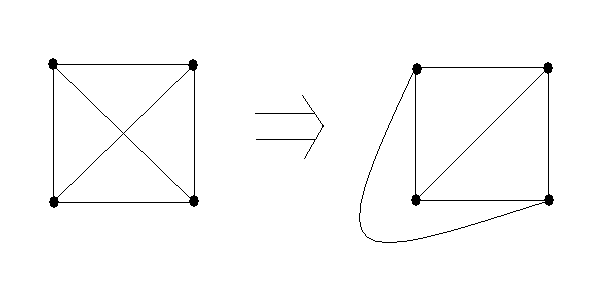
A more interesting example is below

Some of the applications of Graph Isomorphism are verification of computer programs, Security, for example fingerprint scanners, facial scanners etc. The problem is in class NP (nondeterministic polynomial time) mean given a solution (bijective mapping) you can verify the solution efficiently.

#Combinatorics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Can the graph isomorphism problem be solved in polynomial time?

Agnishom Chattopadhyay - 4 years, 6 months ago

till now no one is able to solve the problem in polynomial time in general (For some special class of graphs it is solvable in polynomial time like for trees)

shivdutt sharma - 4 years, 6 months ago

Note: Laszlo Babai showed last year that Graph Isomorphism is in Quasipolynomial-time.

Calvin Lin Staff - 4 years, 5 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$