Half Tau Day is Fast Approaching!

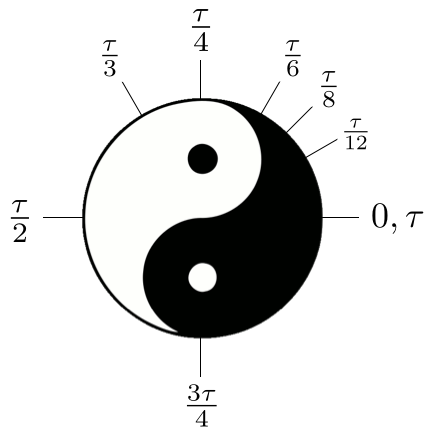
Hello all! I hope you're all gearing up for $\frac{\tau}{2} = \pi $ day! I am a giant proponent of $\tau$, and you should be too. For those of you who don't know, $\tau = 2\pi$. $\tau$ is a much more natural circle constant, as a circle is, after all, defined by its radius, not its diameter. One can find an incredibly compelling argument for $\tau$ in Michael Hartl's Tau Manifesto. I know I'll be spending Half Tau Day unwillingly participating in $\pi$ activities with my blissfully ignorant peers, who I will inevitably urge to join Brilliant and educate themselves about the marvels of $\tau$ !

Have a safe and happy $\frac{\tau}{2}$ day!

#Geometry #Pi #Circles #Tau

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I feel stupid for asking this but isn't $\pi$ day on $14$ March?

Siddhartha Srivastava - 6 years, 3 months ago

Yeah! This $\pi$ day is special though, because it will be (in the American format of month/day/year) $3/14/15$ . $\tau$ will have its revenge on $6/28/31$ !

Ryan Tamburrino - 6 years, 3 months ago

To be honest they are equally valid, as $\pi$ is better in some situations and $\tau$ is better in others. For example: circumference = $\tau$ r may be easier to deal but then you end up with an area of: $\frac{\tau}{2}$ $r^{2}$ . You may also look at it from a trigonometry point of view... all the trigonometric functions repeat themselves every $\tau$ radians, but then when proving that $\zeta$ (2) = $\frac{\pi^2}{6}$ you need $\pi$ to obtain: $\frac{sin(x)}{x} = \displaystyle\prod_{n=1}^{\infty} (1-(\frac{n\pi }{x})^2)$ and the argument continues....

Curtis Clement - 6 years, 3 months ago

I will concede a few small victories to $\pi$ , including that one that you mentioned regarding the $\zeta$ function. However, if you look at the Tau Manifesto, Hartl shows that area of a circle with $\tau$ follows other quadratic forms of other formulas from physics. So, that $\frac{1}{2}$ out in front isn't quite as unnatural as it seems.

Ryan Tamburrino - 6 years, 3 months ago

Maybe there ought to be a friendly Tau vs pi debate

Curtis Clement - 6 years, 3 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$