Help?

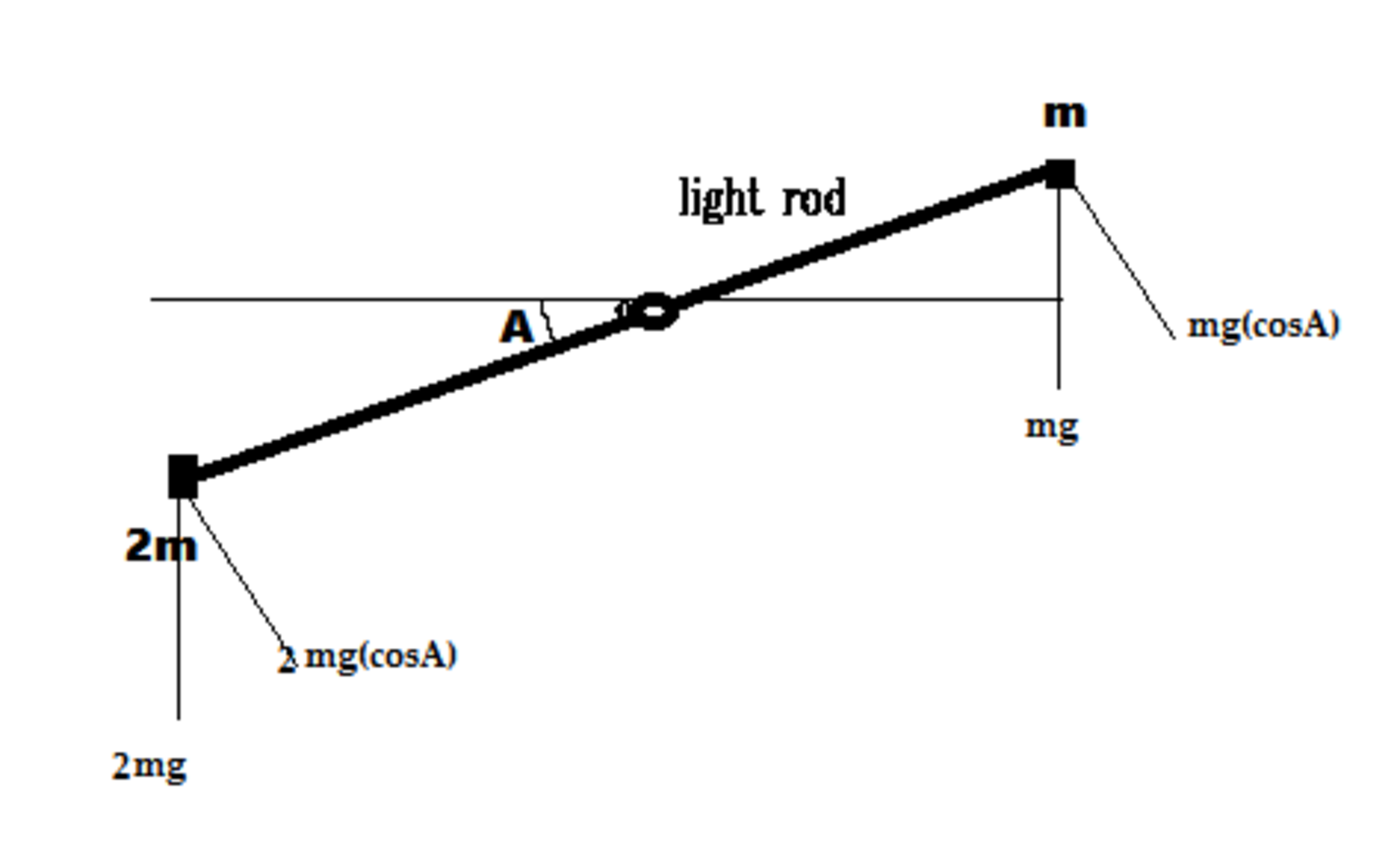
Here's the question.......Two point masses m and 2m are attached at each end of a light rod. The rod is pivoted at the center and is free to move in a vertical plane. Then find the angle "A" when the system is in equilibrium position. And feel free to consider any additional information, you think I forgot to mention.

My doubt goes like this......the gravitational force will be more on its left arm than that of right and hence the torque. So what I think is the rod should attain vertical position with the mass "2m" at the bottom. But that ain't what happens. Tell me where I'm wrong.

#Rotation #RotationalMotion

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

This is an excellent question. Before giving an answer I would first ask you to perform the same experiment with a pencil (one that has not got its writing end sharpened). Place its midpoint on your finger and you will be able to balance it. Now stick a chewing gum at one end and observe that it topples. So see, your explanation regarding equilibrium at the vertical position works perfectly in this case. Then why not the common balance? The answer lies in its construction. In a common balance, weights don't stick to the two ends (like what you may call a mass dipole). They hang from the two ends. This makes the center of mass of the whole system somewhat below its center of rotation. And since common balances are in translational equilibrium, we are only to calculate the torque about the center of mass to study the system's rotation. Here, you were calculating the torque about the center of rotation, where lies the fallacy. Observe, that when both the ends have equal weights hanging from them, center of mass lies on the vertical line below the center of rotation. But once you hang two different weights from two ends, the center of mass shifts from the vertical line, towards the mass which is heavier. Now if you calculate the torque about this shifted center of mass, you will see that what happens in real life is perfectly normal and the tilted position of the balance that you have drawn is the equilibrium position. For further reference see my post on the physical balance problem. hope this helped you.

Kuldeep Guha Mazumder - 5 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$