HELP

A Question that I need help for

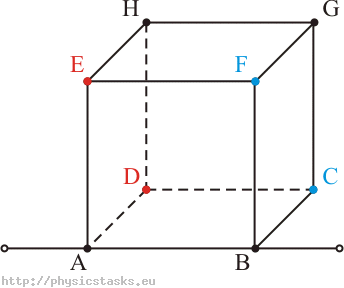
A cube has its vertex named A,B,C,D,E,F,G,H. All of them are real positive numbers. A near sum is the sum of all numbers of the vertexes that connects to the original vertex. The value of the near sums are (3,6,9,12,15,18,21,24). If the value of the near sum of A is 1, then what is the value of the near sum of F?

#Algebra #MathCompetitions

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Just to clarify, is $1$ the near sum of $A$ or the value of $A?$ Because it seems that there are exactly 8 near sums you listed out, none of which are $1.$

Steven Yuan - 6 years, 4 months ago

@Steven Yuan Probably a typo ("near sum of $A$ is 12/15/18"?).

@Alfian Edgar Notice that the near sums have complements which sum to 27, ie the near sum of a vertex is 27 minus the near sum of the opposite vertex; shouldn't be too hard to prove. Then, $nearsum(F) = 27-nearsum(A)$ .

But if $A = 1$ , then I don't know. My brain isn't working today.

Jake Lai - 6 years, 4 months ago

lol, then nearsum(F)= 27-3 = 24

math man - 6 years, 4 months ago

I'm sorry, what I meant was near sum of a=3, the original question was using the average of the near sums lol. It's my mistake.

Alfian Edgar - 6 years, 4 months ago

Then hopefully my reply to Steven will help you out a bit. Good luck and happy solving!

Jake Lai - 6 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$