Help: Continuity of function

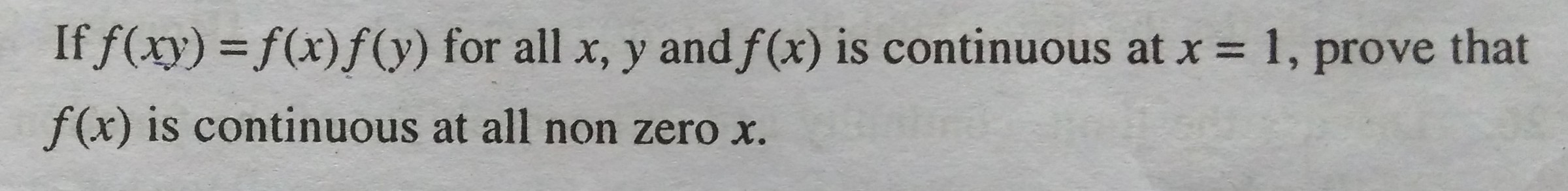
Moderator's edit:

Given that $f(x)$ is a function continuous at $x=1$ and satisfy the functional equation $f(xy) = f(x) f(y)$ for all $x$ and $y$ . Prove that $f(x)$ is continuous at all non-zero $x$ .

#Calculus

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$f(1)^2 = f(1) \Rightarrow f(1) = 1, \text {or } f(1) = 0. \\ f(1) = 0 \Rightarrow f(x) = 0 \text{ } \forall \text{ } x \in R \Rightarrow \text{f is continuous over R. Otherwise, } f(1) = 1. \\~\\ \text{Suppose we had a sequence of real numbers, } (a_n), \text{ such that, } \lim_{n\to\infty} (a_n) = 1. \\ \text{The existence of such a sequence is guaranteed by the density of real numbers.} \\ \text{Now f is continuous at 1, so, by the definition of continuity, } \\ \lim_{n\to\infty} f((a_n)) = f(\lim_{n\to\infty} (a_n)) = f(1) = 1. \\~\\ \text{Take an arbitrary real number, } c \text{. Now, } \\ \lim_{n\to\infty} (c \cdot a_n) = c \cdot \lim_{n\to\infty} (a_n) = c. \\ \text{So, } f(c) = f(c) \cdot 1 = f(c) \cdot (\lim_{n\to\infty} f(a_n)) = \lim_{n\to\infty} f(c) \cdot f(a_n) = \lim_{n\to\infty} f(c \cdot (a_n)). \\ \text{But, } \lim_{n\to\infty} c\cdot (a_n) = c. \\ \text{So, as } n \to\infty, c \cdot a_n \to c \text{. Set } c \cdot a_n = x. \text{ Then, } \lim_{x \to c} f(x) = f(c)\text{, which is what we needed to show. } \\~\\ \text{This finishes the proof! I like your questions, Akhilesh. }$

Ameya Daigavane - 5 years, 3 months ago

Can you please provide a solution for this one too.@Rishabh Cool

Akhilesh Prasad - 5 years, 4 months ago

e raised to x

Asif Mujawar - 5 years, 4 months ago

I dont think ${ e }^{ x }$ can be the answer as it is continuous at $x=0$ too. Please a provide a solution if you have arrived at this answer.

Akhilesh Prasad - 5 years, 4 months ago

@parv morCan you please post a solution to this one too

Akhilesh Prasad - 5 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$