Help me!!

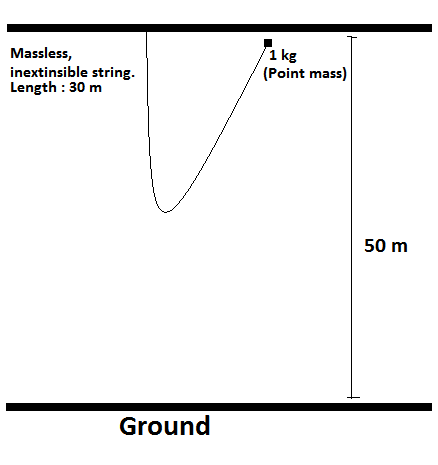
Consider the situation as shown in the figure. When the point mass (1 kg) is released, it will start accelerating downwards due to gravity and by the time it moves through 30 m it will rebound upwards due to the string. Find the maximum height it reaches. Consider ideal conditions.

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

EDITED

The horizontal distance was 30cm

Now let us consider the system ,, Let us make the following observations--

1) Initially there was no tension in string as it wasnt taut

2) So the mass falls vertically freely under gravity till it becomes taut.

3) And since the mass was not at the same position as that of hinge initially,, surely it would not become taut 3m below the hinge point

4) When it becomes taut,, the ball's component of velocity paralell to the string becomes 0 , and the other component that is perpendicular to it remains (can be established through angular momentum conservation) (or qualitatively)

5) So the remaining energy of ball will bring it up again and from there we can decide the maximim height it reaches

So heres what i think is gonna happen, Please Check if i am correct

When the ball falls vertically till string becomes Taut, Applying energy conservation-- (note the $\theta$ is the angle between string and vertical when it becomes taut)

$mglcos\theta \quad =\quad \frac { m{ v }^{ 2 } }{ 2 }$

Now it falls vertically till then, so its velocity will be downward,, so its component perpendicular to string is

$v\quad sin\theta \\ \\ \quad$

which is

$\sqrt { 2glcos\theta } sin\theta$

Now with this velocity it continues further motion as a circle about the hinge point,, thus again applying energy conservation

we get

$mglcos\theta \quad (sin\theta )^{ 2 }\quad =\quad mgh\quad \\ h=lcos\theta \quad (sin\theta )^{ 2 }$

Now as the lateral distance is 30 cm ,, so the angle $\theta$ is approx 37 degrees,, (thats irrelevant,, let it be arc sin (0.6) ) either way it means the answer is 72/5 cm,,

@Ronak Agarwal am i correct, if answer does not matter, just tell if there is anything wrong with the method,, thankyou

NOTE - I assumed that as string is inextensible,, the whole component of velocity paralell to it is cancelled (that is no rebounce occurs, or string does not behave as a spring even for a second)

Mvs Saketh - 6 years, 7 months ago

According to my calculation the answer should be :

${ h }_{ ground }\quad =\quad 50\quad -\quad 30{ (\cfrac { \sqrt { { 30 }^{ 2 }-{ d }^{ 2 } } }{ 30 } ) }^{ 3 }$ .

where d = initial distance of the Point mass from the point of suspension.

And I think 'd' should be mentioned in this question.

here is diagram of this question: ( it is rough figure don't take it seriously :P )

Diagram Diagram

Deepanshu Gupta - 6 years, 7 months ago

I got the same answer.

Ronak Agarwal - 6 years, 7 months ago

@Mvs Saketh

Actually the horizontal distance is 30 cm and the length of the string is 50 cm . It is given wrong in the diagram. Now can please you please post your solution again then it can be checked whether it is correct or not.Refer to the values given by me. I know this question as I have said I have seen it in fiitjee grandmasters package.

Ronak Agarwal - 6 years, 7 months ago

I have edited it accordingly, check now

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – Also the question was asking the speed of the ball at the lowest point.

Ronak Agarwal - 6 years, 7 months ago

Your method is absolutely correct @Mvs Saketh this is the correct method needed to solve the question.

But can you solve for the velocity at the lowest point of the trajectory.

Ronak Agarwal - 6 years, 7 months ago

Yes i will use conservation of energy again after the "Taut" instant because the tension in string only acts perpendicular to the direction of motion after it has become taut and thus does no work,, so i will use change in mgh= gain in KE and find out

Mvs Saketh - 6 years, 7 months ago

see if we consider just vertical motion then when the string becomes taut it'll provide impulse to the particle in opposite direction to its motion (i.e., upward direction) , then what do you think the value of the impulse will be.??

Shantanu Lautre - 6 years, 7 months ago

No please observe my answer carefully,, impulse is not provided in vertical direction but along the string,, (tension acts along the string ) so the component of velocity paralell to string gets cancelled completely or the impulse provided is the momentum of the particle along the string which is mvcos(x) ,,, see my solution carefully ,

Mvs Saketh - 6 years, 7 months ago

@Mvs Saketh – Gotcha.......Thank you a million.!

Shantanu Lautre - 6 years, 7 months ago

I got that too......

Shantanu Lautre - 6 years, 7 months ago

This question I saw in grand masters package of fiitjee.

Ronak Agarwal - 6 years, 7 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$