HELP: what is value of the angle?

Hello, I want to find the angle accurately. Please help me out.

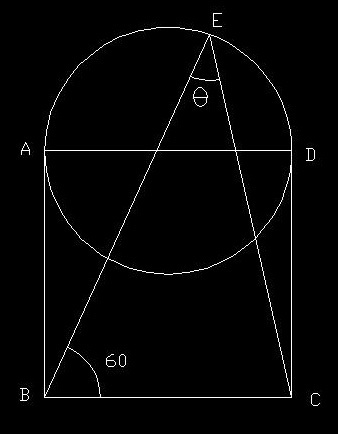
ABCD is a square and AD is the diameter of the circle. what is the value of θ \theta ?

I think θ \theta is independent of the length of the sides of the square and am getting an answer approximately 40.183 degrees. I got the answer by solving some properties of triangle equations and doing some constructions. I don't know whether it is right or wrong. My question is what is the exact angle? And can we get the angle by means of constructions only (I mean without using a calculator because in my case I needed to calculate huge surds:-\ )?

Thanks in advance.

#Geometry

Note by Ankan Bairagi
2 years, 7 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Suppose the side length of the square is 1. The circle equation is:

(x−12)2+(y−1)2=14 \Big(x - \frac{1}{2} \Big)^2 + \Big(y-1 \Big)^2 = \frac{1}{4}

Suppose point B is the origin. Define a direction vector:

vx=cos 60∘vy=sin 60∘v_x = cos \, 60^\circ \\ v_y = sin \, 60^\circ

Substitute into the circle equation:

(α vx−12)2+(α vy−1)2=14 \Big(\alpha \, v_x - \frac{1}{2} \Big)^2 + \Big(\alpha \, v_y-1 \Big)^2 = \frac{1}{4}

The remaining steps are:
1) Expand to get a quadratic equation in α\alpha
2) Solve for α\alpha. Note that you must solve for the greater alpha value
3) (Ex,Ey)=(α vx,α vy)(E_x, E_y) = (\alpha \, v_x, \alpha \, v_y)
4) Calculate vectors from E to B and E to C
5) Given those two vectors, use the dot product formula to calculate θ\theta. In other words, take the arc-cosine of a quantity equal to the dot product divided by the product of the vector magnitudes.

This yields θ=37.9235∘\theta = 37.9235^\circ

Steven Chase - 2 years, 7 months ago

Log in to reply

Taking B B as the origin is really clever

Henry U - 2 years, 7 months ago

Nice solution! I did a mistake in the calculation. The equations were really messy. I am also getting 37.9 degree. Thank you so much!!!!

Ankan Bairagi - 2 years, 7 months ago

I got approximately 37.9235°, but I'm really not sure because the exact formulas get really messy.

First, I put the construction into a coordinate system with the center of the circle at the origin and 1 unit as the radiua of the circle. Every point on this circle can be written as (cos⁡α,sin⁡α) (\cos \alpha, \sin \alpha) , where α \alpha is the central angle.
Then I considered the slope of line DE DE . It is given as 60∘=3 60^\circ = \sqrt{3} , but we can also write it as ΔyΔx=sin⁡α+2cos⁡α+1 \frac {\Delta y}{\Delta x} = \frac {\sin \alpha + 2} {\cos \alpha + 1} . If we set these two equal to each other, we can solve for α \alpha and get α=2arctan⁡(−12+3−34) \alpha = 2 \arctan\left(- \frac 1 2 + \sqrt{\sqrt{3}-\frac 3 4}\right) .
Now we can plug this into E=(cos⁡α,sin⁡α) E = (\cos \alpha, \sin \alpha) and get E=(−34+123−34,−12+143+123−94) E = \left(-\frac34+\frac12\sqrt{\sqrt{3}-\frac34}, -\frac12+\frac14\sqrt{3}+\frac12\sqrt{\sqrt{3}-\frac94}\right) .
Then we can calculate the slope of line EC EC as 6+3+123−9−7+23+43−3 \frac {6+\sqrt{3}+\sqrt{12\sqrt{3}-9}} {-7+2\sqrt{3}+\sqrt{4\sqrt{3}-3}} .
If we take the inverse tangent of this we get the angle at C C which we subtract from 180∘−60∘ 180^\circ - 60^\circ to get our final answer of 2π3+arctan⁡(−94−3−12814+123)≈37.9235∘ \frac{2\pi}3+\arctan\left(-\frac94-\sqrt{3}-\frac12\sqrt{\frac{81}4+12\sqrt{3}}\right) \approx 37.9235^\circ .

As I said, it gets really complicated and I'm not sure if I've calculated it correctly but I think the way I did it is right.

Henry U - 2 years, 7 months ago

Log in to reply

I got the same answer. My solution is above

Steven Chase - 2 years, 7 months ago
×

Problem Loading...

Note Loading...

Set Loading...