How does one find the area of this?

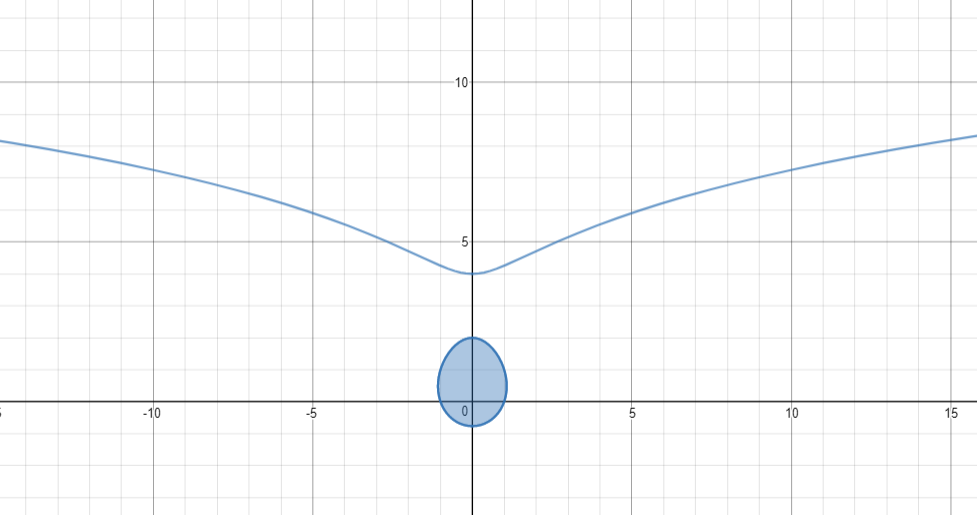
Hello everyone! The relation of the image above is $x^2+y^2 = 2^y$ . How do you find the area of the egg shape?

*Note: There is a section above the droplet, which should not be accounted for.

Made with Desmos graphing calculator

#Calculus

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

A different question about this graph: Consider graphs of the form $x^2+y^2=a^y$ . If $a=2$ , the graph is as above. If $a=2.09$ , the egg shape is now connected to the upper segment of the graph but if $a=2.08$ , the egg shape is still distinct. Therefore, at what value of $a$ does this egg first connect to the upper part of the graph?

kb e - 3 years, 5 months ago

Actually, that question has a precise answer: $a = e^{2/e} \approx 2.0871$ .

$x^2 + y^2 = a^y.$

At the transition point, the tip of the "egg" and the dip in the rest of the graph meet each other; due to symmetry, this must happen somewhere on the line $x = 0$ , and the connection will have a vertical tangent. Thus we set $dx = 0$ in the total derivative and substitute $a^y = y^2$ :

$2x\:dx + 2y\:dy = (\ln a) a^y\:dy$ $2y = (\ln a) a^y = (\ln a)y^2.$ $\ln a = \frac 2 y\ \ \ \therefore\ \ \ a = e^{2/y}.$

Now substitute $x = 0$ and this result in the original equation: $y^2 = a^y = (e^{2/y})^y = e^2;$ $y = e,\ a = e^{2/e}.$

Arjen Vreugdenhil - 3 years, 5 months ago

You can also generalize this solution for graphs of the form $x^{2n}+y^{2n} = a^y$ . The general solution for the critical $a$ is $a = e^\frac{2n}{e}$

kb e - 3 years, 5 months ago

whfhbbjwhf