How to Count Rectangles!

Hi there! Me again. *munches*

Sorry, I still haven't finished my hamburger since the last time we count squares, I hope you don't mind that.

Anyway, we are here to see how to count rectangles of a certain size in a grid.

Consider this question: How many $3\times2$ rectangles are there in the $4\times5$ grid below?

I'm a little bit picky here, note that dimensions here are expressed as width $\times$ height, so in this case I only want $3\times2$ rectangles (that is, a rectangle of width 3 and height 2) and not the $2\times3$ ones.

If we mark an 'X' on every bottom-right corner of every $3\times2$ rectangle, we would see this:

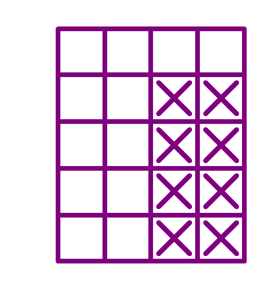
Hey, that means counting the number of $3\times2$ rectangles in the original grid is the same as counting how many X's are there, or in other words, it is the same as counting the number of unit squares in an $2\times4$ grid.

There are $2\times4=8$ unit squares in a $2\times4$ grid, therefore, the number of $3\times2$ rectangles in the original grid is 8! Hooray!

*munches*

Mmm... so in general, how many $x\times y$ rectangles ( $x$ is the width of the rectangle, $y$ is the height of the rectangle) are there in an $a\times b$ grid ( $a$ is the width of the grid, $b$ is the height of the grid), given that $x\leqslant a$ and $y\leqslant b$ ?

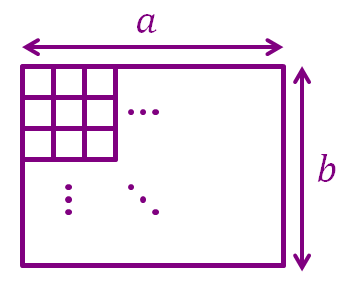
Again imagine marking an 'X' on every bottom-right corner of every $x\times y$ rectangle, we will get a grid full of X's.

The width of the "X grid" is $a-x+1$ , while the height of the "X grid" is $b-y+1$ .

Since the number of $x\times y$ rectangles in an $a\times b$ grid equals the number of unit squares in the "X grid", hence the number of $x\times y$ rectangles in an $a\times b$ grid is $(a-x+1)(b-y+1)$

*munches*

The number of $x\times y$ ( $x$ is the width of the rectangle, $y$ is the height of the rectangle) rectangles (the exact $x\times y$ rectangle, not including rotated variations such as $y\times x$ ) in an $a\times b$ grid ( $a$ is the width of the grid, $b$ is the height of the grid) provided that $x\leqslant a$ , $y\leqslant b$ is $(a-x+1)(b-y+1)$

This is one part of Quadrilatorics.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I think another way to do it is breaking them up. For example, if we want to count the number ot rectangles in $10×10$ grid, is first counting the number of rectangles in $10×1$ grid then xounting the number of rectangles in $10×2$ grid, then in $10×3$ , and so in, in this way we would be able to establish a pattern in the number of rectangles, and by arithmetic/geometric progression, we would het the answer.

Ashish Menon - 5 years, 2 months ago

Yes, but in this case I only want to count rectangles of a specific size.

Kenneth Tan - 5 years, 2 months ago

We can do in that case too. Your questions are awesome.

You may see the solution of my problem to see my approach.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$