How to Count Squares!

Let me go grab a hamburger real quick...

Ok, I'm back.

How many squares are there in the $6\times4$ grid below? That's a reaallly good question!

Let's start by counting the smallest $1\times1$ squares, this is just the same as counting the number of unit squares in a $6\times4$ grid, there are $6\times4=24$ 1 by 1 squares in the grid.

Now let's move on to the $2\times2$ squares, notice that counting the number of $2\times2$ squares in a $6\times4$ grid is just the same as counting the number of unit squares in a $5\times3$ grid. So the number of 2 by 2 squares in the grid is $5\times3=15$.

Now the $3\times3$ squares, similarly, counting the number of $3\times3$ squares in a $6\times4$ grid is just the same as counting the number of unit squares in a $4\times2$ grid, which is $4\times2=8$.

And again the number of $4\times4$ squares in a $6\times4$ grid is equal to the number of unit squares in a $3\times1$ grid, which is $3\times1=3$.

Add up all the number of squares together: $24+15+8+3=50$. Tada! We now have our answer! There are 50 squares in a $6\times4$ grid.

Mmm... the hamburger is really good...

Back on topic, in general, what is the total number of squares in an $a\times b$ grid (where $a$ is the width of the grid and $b$ is the height of the grid), given $a\geqslant b$?

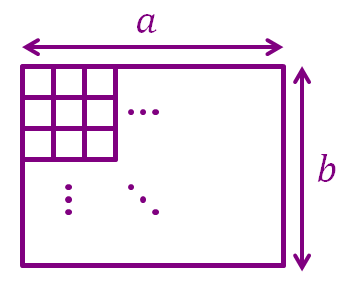
Again let's start from the $1\times1$ squares, that's trivial, there's $ab$ of them.

Now moving on to the $2\times2$ squares, the number of $2\times2$ squares in an $a\times b$ grid is equal to the number of unit squares in an $(a-1)\times(b-1)$ grid.

Notice the pattern? Counting the number of $n\times n$ squares in an $a\times b$ grid is the same as counting the number of unit squares in an $(a-n+1)\times(b-n+1)$ grid.

The largest square that can contain in an $a\times b$ grid given that $a\geqslant b$ is $b\times b$.

Hence, the total number of squares in an $a\times b$ grid is $ab+(a-1)(b-1)+(a-2)(b-2)+\ldots+[a-(b-2)][b-(b-2)]+[a-(b-1)][b-(b-1)]$ Or $\sum_{i=0}^{b-1}{(a-i)(b-i)}$

This is ugly, we don't like sigma symbols sitting around, so why not we simplify this a little bit...

$\begin{aligned} \sum_{i=0}^{b-1}{(a-i)(b-i)}&=\sum_{i=0}^{b-1}{[ab-(a+b)i+i^2]} \\&=ab^2-\frac{(a+b)b(b-1)}{2}+\frac{b(b-1)(2b-1)}{6} \\&=b\left[ab-\frac{ab-a+b^2-b}{2}+\frac{2b^2-3b+1}{6}\right] \\&=\frac{b}{6}\left[6ab-3ab+3a-3b^2+3b+2b^2-3b+1\right] \\&=\frac{b}{6}\left[3ab+3a-b^2+1\right] \\&=\frac{b(b+1)(3a-b+1)}{6} \end{aligned}$ BOOM! There we have it! *Round of applause* *Fireworks* *Pancakes*

The total number of squares in an $a\times b$ grid (where $a$ is the width of the grid and $b$ is the height of the grid), given $a\geqslant b$ is $\frac{b(b+1)(3a-b+1)}{6}$

If $a<b$, then we just swap $a$ and $b$.

Special case: If $a=b$, the above equation becomes $\frac{a(a+1)(2a+1)}{6}$ which is the formula for the sum of squares from 1 to $a$.

Done! Now let me finish my burger...

This is one part of Quadrilatorics.