I discovered a TONCAS 1

I made a simple configuration , whose converse is also true. Though the proof is very easy , the important thing is that its converse is also true!

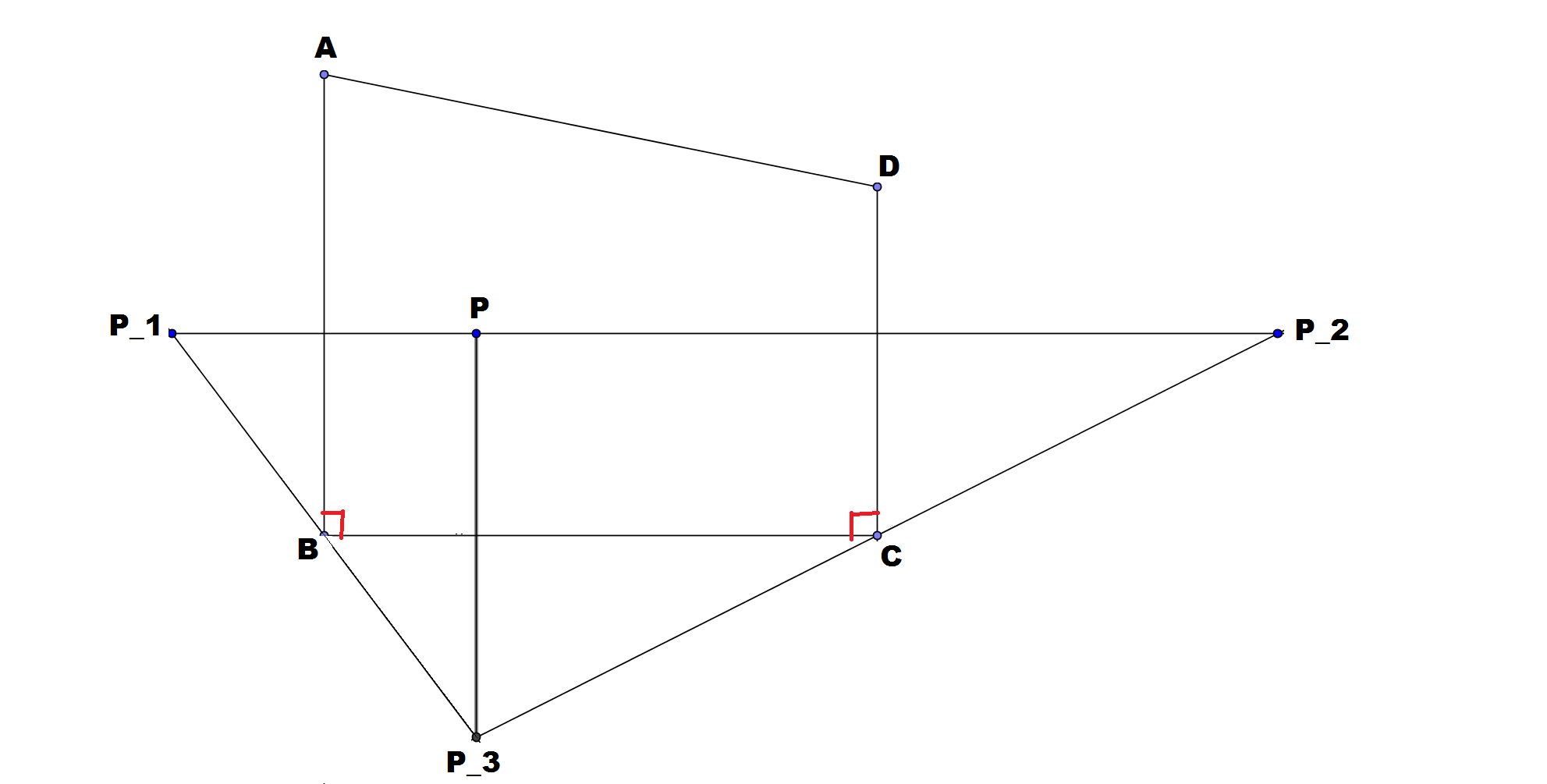
Problem statement: Let $AB \perp BC$ , $DC \perp BC$ . Consider a point $P$ inside $ABCD$ . Let $P_1$ be its reflection in $\overline{AB}$ and $P_2$ be its reflection in $\overline{CD}$ . Let $\overrightarrow{P_1B} \cap \overrightarrow{P_2C} = {P_3}$ . Prove that $\overline{P_3P} \perp \overline{P_1P_2}$ .

Statement converse: Consider a quadrilateral $ABCD$ . Consider a point $P$ inside $ABCD$ . Let $P_1$ be its reflection in $\overline{AB}$ and $P_2$ be its reflection in $\overline{CD}$ . Let $\overrightarrow{P_1B} \cap \overrightarrow{P_2C} ={P_3}$ . If $\overline{P_3P} \perp \overline{P_1P_2}$ , then prove that $AB \perp BC$ , $DC \perp BC$ .

I have my own solution too. Please post awesome "complete" solutions below. Enjoy!

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

The very next revolutionary book in the history of mathematics - Nihar's treatises on Euclidean Geometry.

Swapnil Das - 6 years ago

Well , I think you over-understood me as the best in geometry. I am just "good" at geometry since its one of my interests. Anyway , thanks!

Nihar Mahajan - 6 years ago

Do you have any other postulates which you have kept a secret?

Swapnil Das - 6 years ago

@Swapnil Das – I have one more ,I will be posting it soon on Brilliant. Actually , its the extension of this configuration.

Nihar Mahajan - 6 years ago

@Nihar Mahajan – It will be a success! Bye!

Swapnil Das - 6 years ago

@Calvin Lin @Azhaghu Roopesh M @Trevor Arashiro @Sharky Kesa Please see my discovery. Thanks!

Nihar Mahajan - 6 years ago

Since points A and D are "essentially useless" other than saying that we have parallel / perpendicular lines, you should remove them from the statement.

Calvin Lin Staff - 6 years ago

Uum ... I have points $A,D$ just for labeling the angles , segments , that is for notation convenience. I am not able to understand why are you saying to remove them.

Nihar Mahajan - 6 years ago

Get rid of "right trapezoid such that ....", and list the important information as $AB\perp BC$ , $BC \perp CD$ .

Calvin Lin Staff - 6 years ago

@Calvin Lin – Oh , I see. Thanks for telling that.Lemme edit it.

Nihar Mahajan - 6 years ago

@Calvin Lin – Thanks! I have edited it accordingly. Please tell more of your opinions about it (if any).

Nihar Mahajan - 6 years ago

@Nihar Mahajan – There is no point in saying "Join AD" is there? The idea is to remove irrelevant information like that, so that you're left with just the important attributes. This will make it easier to apply in other scenarios (where there isn't clearly a rectangular trapezoid).

Calvin Lin Staff - 6 years ago

@Calvin Lin – Oh , I completely understood what your intention was. I would definitely take care about this when I will post the extension of this configuration soon. "stay tuned" :P

Nihar Mahajan - 6 years ago

Congrats! xD

Mehul Arora - 6 years ago

It's really nice seeing you discovering postulates at such an age.

Swapnil Das - 6 years ago

Actually this is not a postulate. This is a simple configuration whose converse is also true. Postulates/axioms are just defined and not proved. They are "used" to prove things.

Nihar Mahajan - 6 years ago

What's a TONCAS 1?

Btw, the proof is simple for the positive statement. Just uses scale factors and similar triangles. And by proving the positive, the converse is proved here. I'm curious as to what your extension is. At any guess, I'd say reflecting a point about two parallel lines and having the three points form a right triangle about the intersection of the two lines.

Trevor Arashiro - 6 years ago

No the extension is something else. "Stay tuned" I will post it soon.

Nihar Mahajan - 6 years ago

Mm, $k^2$ . You piqued my interest.

Trevor Arashiro - 6 years ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$