I Drew a Tesseract (Without even knowing how)

We all know that a tesseract (hypercube) is a 4D object analogous to a 3D cube or a 2D square. I decided that I wanted to draw one, despite the fact that I have no idea how. I did know, however, that an edge of a cube is a set of points in which two out of the three spatial coordinates are extremal (relative to the cube's size), and one can vary continuously between the extremes.

What if we did the same thing for a 4D hypercube? Create regions of points where three out of the four spatial dimensions are at extreme values, and only one can vary continously. I wrote a program based on the following processing:

1) Conceptualize a 4D coordinate system (x,y,z,w)

2) Randomly generate a set of four 4D orthogonal basis vectors. These vectors make the plots more interesting than they presumably would be if we used the simple (1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1) set. See the attached code for these vectors.

3) Each plotted point is a weighted sum of the vectors from Step 2, where each basis vector has its own weight

4) Randomly generate the weights so that three of them are at extreme values (either +1 or -1), and the remaining weight varies continuously between -1 and +1. This gives us points along the edges of the 4D hypercube.

5) Make scatter plots with two of the four dimensions. Plotted combinations are xy, xz, xw, yz, yw, zw.

Plots and code are below. I think the first and the sixth plots are the coolest to look at. These are 2D projections of 4D hypercubes, generated purely from randomly generated points. They are not super high-res because I didn't want to put too many points into Excel.

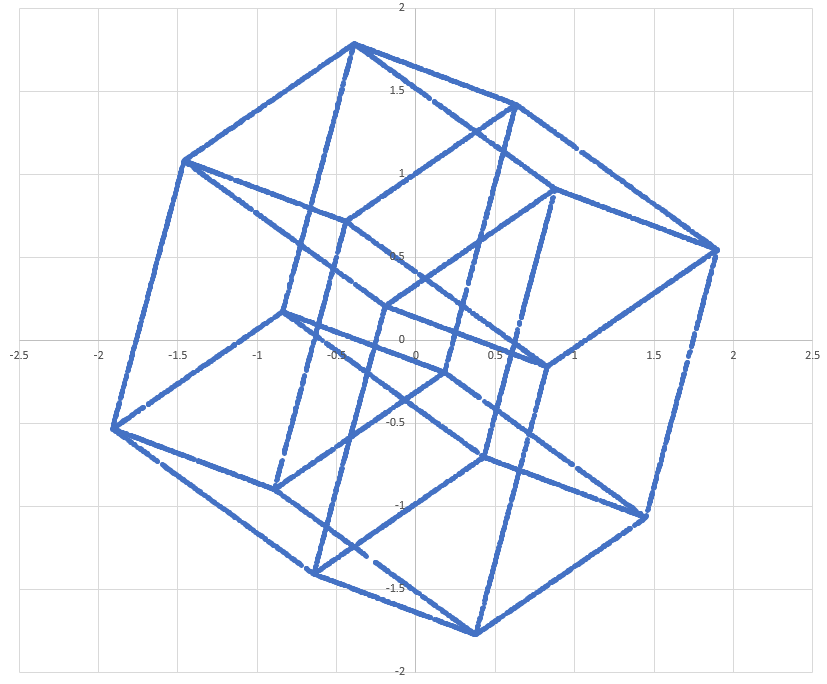
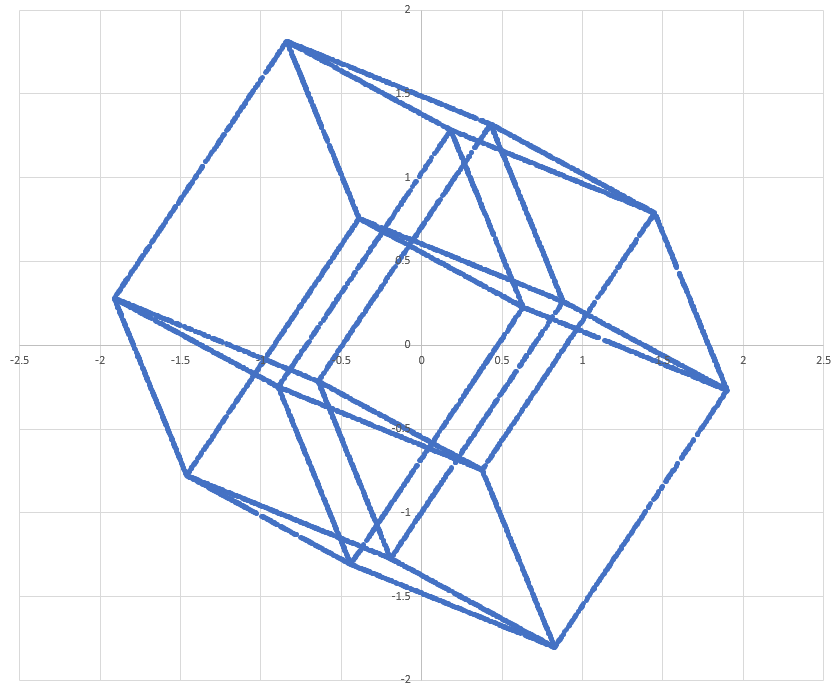
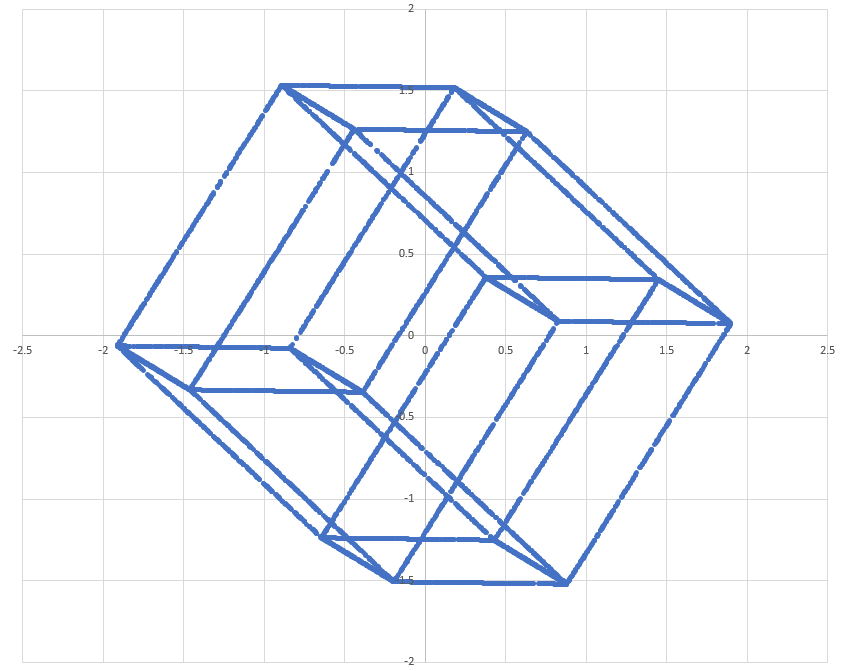
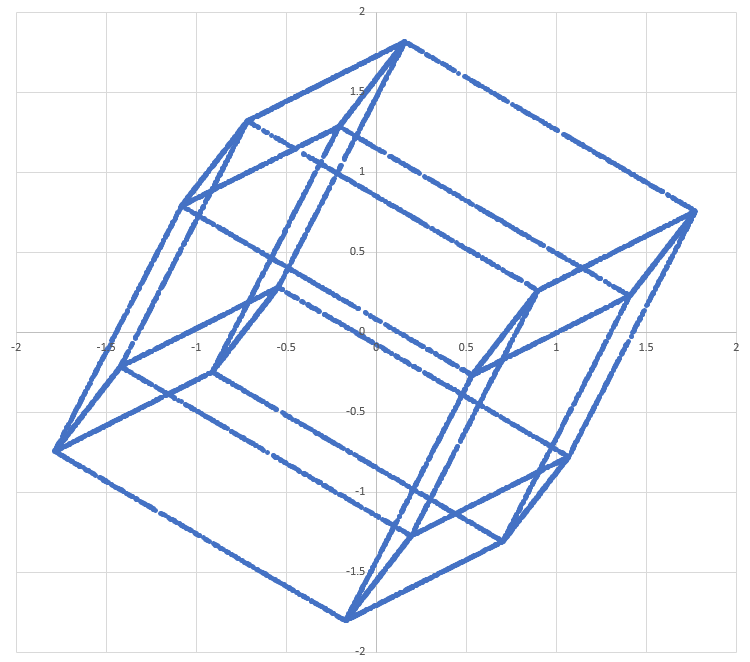
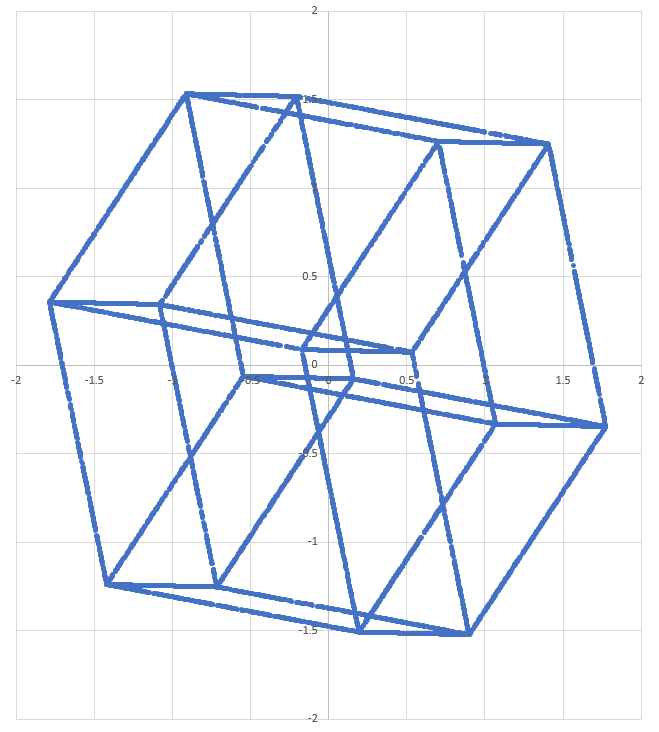
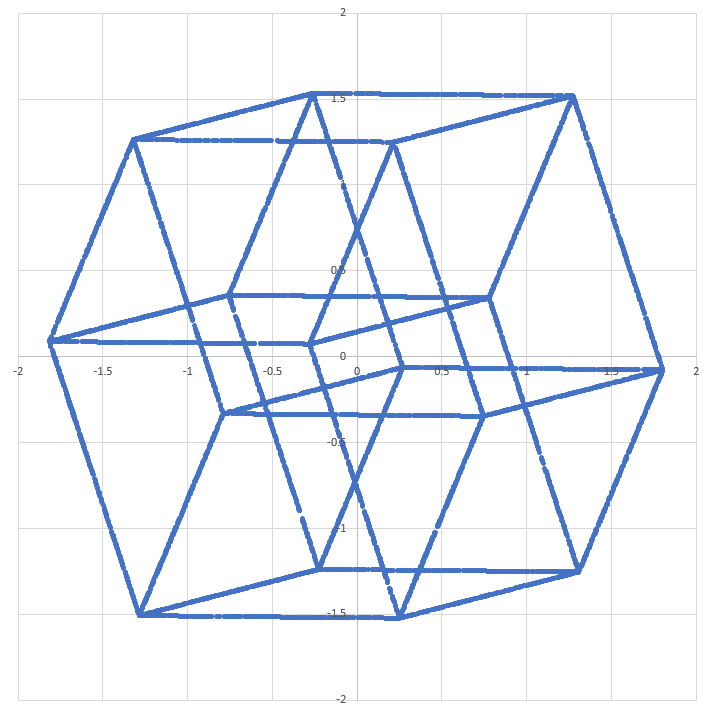
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

import math
import random

sx = 0.509967921254
sy = -0.18278826241
sz = -0.264779918013
sw = 0.797754978662

tx = 0.536030522728
ty = 0.352271346186
tz = 0.767147895871
tw = -0.00734503318408

ux = 0.225111754835
uy = 0.806999040406
uz = -0.529133775059
uw = -0.134618545946

vx = 0.633989716835
vy = -0.437354662725
vz = -0.247769765951
vw = -0.587716669068

for j in range(0,10**4):

    var = random.randint(1,4)

    if var == 1:

        s = random.uniform(-1.0,1.0)

        t = (-1.0)**(random.randint(0,1))
        u = (-1.0)**(random.randint(0,1))
        v = (-1.0)**(random.randint(0,1))

    if var == 2:

        t = random.uniform(-1.0,1.0)

        s = (-1.0)**(random.randint(0,1))
        u = (-1.0)**(random.randint(0,1))
        v = (-1.0)**(random.randint(0,1))

    if var == 3:

        u = random.uniform(-1.0,1.0)

        s = (-1.0)**(random.randint(0,1))
        t = (-1.0)**(random.randint(0,1))
        v = (-1.0)**(random.randint(0,1))

    if var == 4:

        v = random.uniform(-1.0,1.0)

        s = (-1.0)**(random.randint(0,1))
        t = (-1.0)**(random.randint(0,1))
        u = (-1.0)**(random.randint(0,1))

    x = s*sx + t*tx + u*ux + v*vx
    y = s*sy + t*ty + u*uy + v*vy
    z = s*sz + t*tz + u*uz + v*vz
    w = s*sw + t*tw + u*uw + v*vw

    #print x,y
    #print x,z
    #print x,w
    #print y,z
    #print y,w
    print z,w