i find this integral problem very interesting !!!
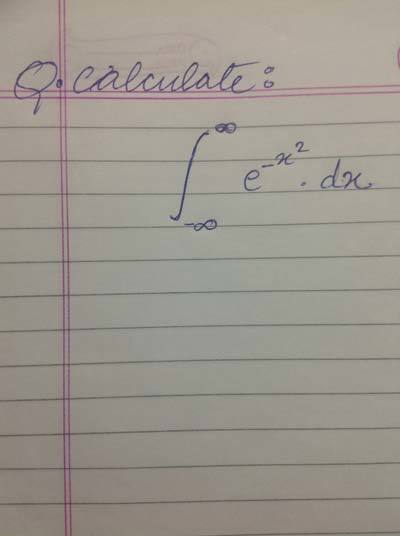
Help on this interesting integral problem ??
No vote yet
4 votes
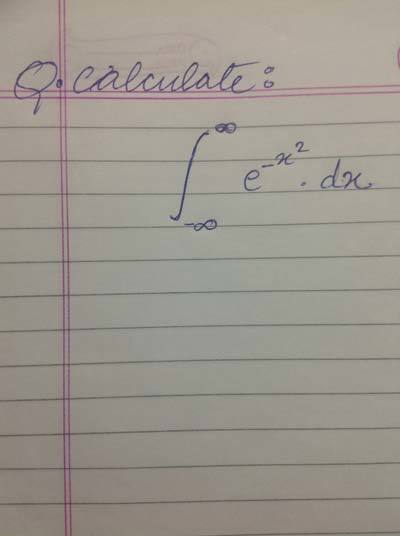
Help on this interesting integral problem ??
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
ya it's cool.you try to find the square of the quantity,with one variable x and the other y.then you integrate them simultaneously,a double integral.It's easy to evaluate once you transform it to polar coordinates.Nice One.Answer is root pi
lower limit is negative infinity..
Log in to reply
is it 0
You can also look up this pdf www.stankova.net/statistics2012/doubleintegration.pdf.
another not-so-cool way is to use gamma function.use the substitution x=root u
squareroot of Pi ? ( Error Function)
As our function is an even function therefore split the limit of integration from -infinity to +infinity as 2 times 0 to infinity and use Gamma function by making a suitable substitution. It can also be done by converting the problem into polar form.
This function is not integrable using the methods we learn till Undergraduate college level. I don't know about what we learn in college...
Although ∫e−x2dx can't be expressed in terms of elementary functions, we can evaluate ∫−∞+∞e−x2dx. Doing so yields π (for justification see http://en.wikipedia.org/wiki/Gaussian_integral#Computation).
It can be solved by GAMMA FUNCTION=integrate(0-infinity)e^-x.x^(n-1)dx for all x>=1 x belongs to Z+!!!
I think ans is 0 .. I think we can solve it using integration by part