I found the value of PI on my own!

This note is an extension to my previous note. In that note, I asked the community to find the mistake in my solution yielding 0=1. In that note, this mistake was the multiplication of inifinty and 0 which is basically an indeterminate form. This note is a correct version of the previous note and my formula seems to give a good approximation for $\pi$ .

For any $n$ sided regular polygon inscribed in a circle of radius $r$ , our objective is to calculate the perimeter of the polygon.

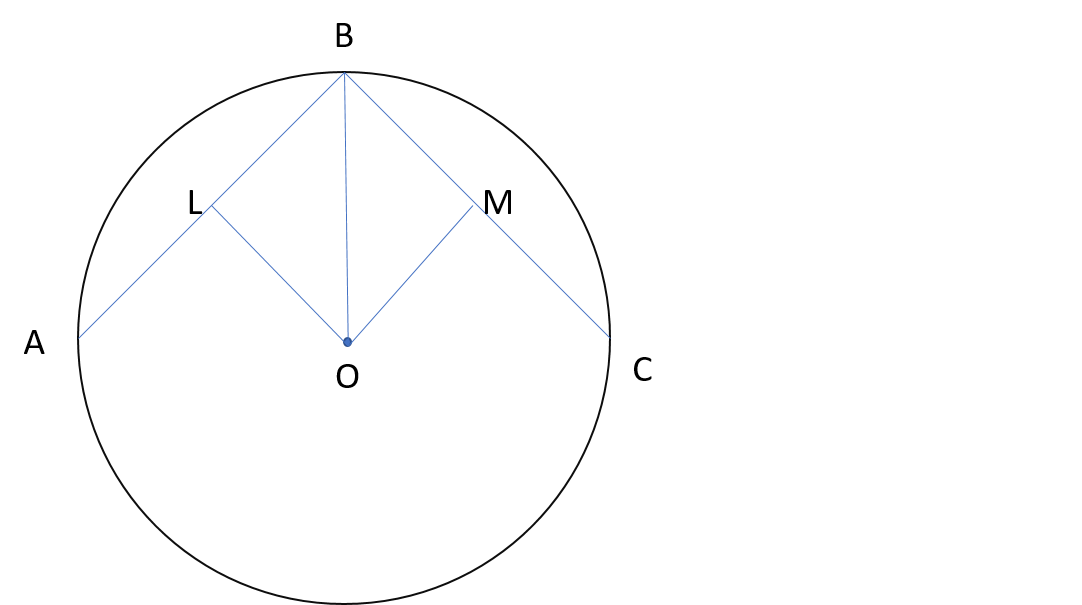
The figure represents the given situation. $O$ is the center of the circle and $AB$ , $BC$ are edges of a regular polygon. $OL$ and $OM$ are perpendiculars drawn on line segments $AB$ and $BC$ respectively. Since perpendiculars from center bisect the chord, thus we have,

$BL = BM$

$OB = OB$

$\angle OLB = \angle OMB$

Therfore by RHS Criteration of congruency, $\Delta OLB \cong \Delta OMB$ .

Thus by CPCT, we have

$\angle LBO = \angle OBM$

For any regular polygon of $n$ sides, each angle is given by $\frac{180(n-2)}{n}$ .

Therefore, $\angle LBM = \frac{180(n-2)}{n}$ . Thus $\angle LBO = \frac{180(n-2)}{2n}$ .

Clearly,

$\frac{BL}{r} = cos(\frac{90(n-2)}{n}°)$

$\ BL = rcos(\frac{90(n-2)}{n}°)$ and thus,

$BC = 2BL = 2rcos(\frac{90(n-2)}{n}°)$

Since it is a regular polygon,

Perimeter = $(n)(BA) = 2nrcos(\frac{90(n-2)}{n}°)$ $.........................(1)$

But as $n$ approaches infinity the polygon tends to coincide the circle in which it is inscribed. Thus in that case the perimeter of the polygon becomes equal to the circumference of the circle in which it is inscribed.

Thus, Comparing the perimeter of the inifinite-sided polygon with the circumference of a circle we get,

$ncos(\frac{90(n-2)}{n}°)=nsin(\frac{180}{n}°) = \pi ......................... (2)$

Let us take a reasonable approximation for $n$ which resembles infinity. Thus, let $n=10^{18}$

Plugging in the value of $n$ in the 2nd equation we get,

$10^{18} \times sin(18 \times 10^{-17}°) = \pi$ which yields us $3.141592653589793238462643383279$ using a scientific calculator which is actually $\pi$ upto 30 decimal places!

Basically, if you want a better approximation just increase the power of 10.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

How did you determine a value for sin?

Scott Keadle - 3 years, 4 months ago

This is the Archimedes's method of calculating $π$ .

Atul Kumar Ashish - 4 years, 5 months ago

I seriously did not know that Archimedes used this method. You can check my previous notes, on how I started to find out Pi. In the previous note the mistake I did was multiplying infinity and zero and wrote it as zero giving me the wrong answer. Today, I realized that instead of taking an infinite value, I can actually use a large finite value.

Akshat Joshi - 4 years, 5 months ago

https://m.youtube.com/watch?v=DLZMZ-CT7YU

I just found that Archimedes did not exactly use this method. Rather he had put polygons inside and outside the circle and compared the outside and inside perimeters to get a range in which Pi lies ( 3.1408 < π < 3.1429 ). And at that time, I feel that the concept of inifinity was not properly developed.

In fact you should read the comments of the video, which proves that this is not Archimedes' method.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$