In a given triangle ABC, a=BC, b=AC, and c=AB where ABC are angle measurements of the triangle. Can you prove that the following inequality is true? Moreover, is there any maximum value of the fraction in the center of the inequality?
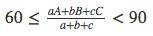
In a given triangle ABC, a=BC, b=AC, and c=AB where ABC are angle measurements of the triangle. Can you prove that the following inequality is true? Moreover, is there any maximum value of the fraction in the center of the inequality?
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
INDONESIA, makassar. abdui,karim
This week, we continue our study of Group Theory with a guest post by Chu-Wee Lim on Lagrange's Theorem.
H=4
Brilliant user Tan asks if it is possible to convert a 4-dimension space to a 3-dimension space in the same way we can convert our 3-dimension world into a 2-dimension map.
6 box
Determine the smallest integer that is divisible by 24 and has digit sum equal to 24.
Since 24 = 8 * 3, the sum of the digits must be = 0 (mod 3), which is satisfied by the fact that the sum of the digits must be 24. Therefore, we ignore this condition, so now we need the smallest n = 0 (mod 8 ), whose sum of digits = 24. We clearly
Brilliant's physics problems this week are all about the hyperloop, a new high-speed transportation system proposed by inventor Elon Musk. The hyperloop is a tube through which capsules move at a top speed of 1,220 kilometers per hour (760 miles per hour). Our problems explore some of the technical challenges it faces as well as the benefits it provides.
6v1 4v1 2v1 2v2 4v1 2v0
6 1 _+ 6
4 1 __+ 5
2 1 _+ 3
2 2 __+ 4
4 1 __+ 5
2 0 __+ 20