Inequality Problem
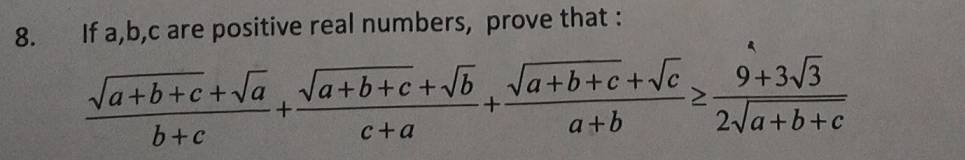
Can any one could help me Solve this problem ?
NOTE: This problem has been taken from KV JMO 2014
No vote yet
1 vote
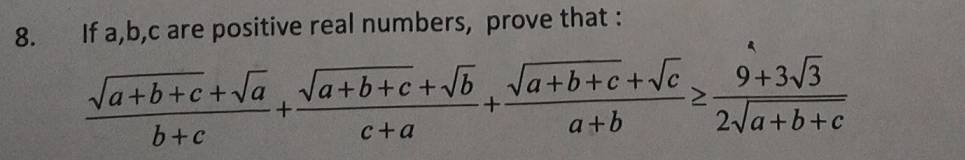
Can any one could help me Solve this problem ?
NOTE: This problem has been taken from KV JMO 2014
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Sorry for bumping this, but I saw that this remained unsolved, so I decided to have a go. From the other comments, it seems like there is a quick solution (given that it is a KV JMO problem, I did not expect it to be so long.) Here we go! (with some help from Wolfram Alpha in Method 2 - but the idea for the function was original, I promise.)
Split the LHS as,a+b+c(a+b1+b+c1+c+a1)+a+bc+c+ab+b+caWe have, by AM-HM or Cauchy-Schwarz (Titu’s Lemma), a+b+c(a+b1+b+c1+c+a1)≥a+b+c⋅2(a+b+c)9=2a+b+c9 The RHS begins to emerge! So we need to show, a+bc+c+ab+b+ca≥2a+b+c33 There are two ways I’ve found to prove this inequality. The first uses normalization and calculus,while the other requires patience to factorize. I’m sorry. Method 1: The given inequality is homogeneous, so we can normalize as,a+b+c=1⇒a,b,c∈(0,1)Now we need to show,1−aa+1−bb+1−cc≥233Let’s focus on one of these terms. If we show, 1−aa≥23a3Then, on addition of the three terms, we get the required inequality. On squaring, this is equivalent to,4a≥27a2(1−a)2⇔27a3−54a2+27a−4≥0 Consider the function, f(x)=27x3−54x2+27x−4On evaluating, we see f(31)=f′(31)=0Also, f(0)<0,f(1)<0Thus, f(x)≤0 ∀ x∈(0,1)But this is what we had to show for a, b and c! ∴1−aa+1−bb+1−cc≥233⇒a+bc+c+ab+b+ca≥2a+b+c33⇒a+b+c(a+b1+b+c1+c+a1)+a+bc+c+ab+b+ca≥2a+b+c9+33And we are done. Method 2: to prove the inequality I was talking about, we show, b+ca≥2(a+b+c)233a3This is equivalent to,(2a−b−c)2(a+4(b+c))≥0So we are done, again - on adding similar terms. Equality holds if, a=b=c.
Noticed that the expression can be written as
a+b+c−a1+a+b+c−b1+a+b+c−c1
Then, by Titu's Lemma, we can combine everything into one term, but I don't know how to approach next. Anyone may continue?
First step is given by Boo. Apply A.M. is greater than equal to H.M. and Cauchy's Inequality. I am not able to use Formatting guide.. Sorry.
Search for the answers by reading books about that topic that may help you on how to solve that problem