Infinite cubic grid of resisrors
Can we find net resistance between the body diagonal points of a infinite cubic lattice
 ?
?
The objective is to find net resistance between A & B of the given cube which is part of infinite grid. Let the resistance between any two adjacent vertices is R
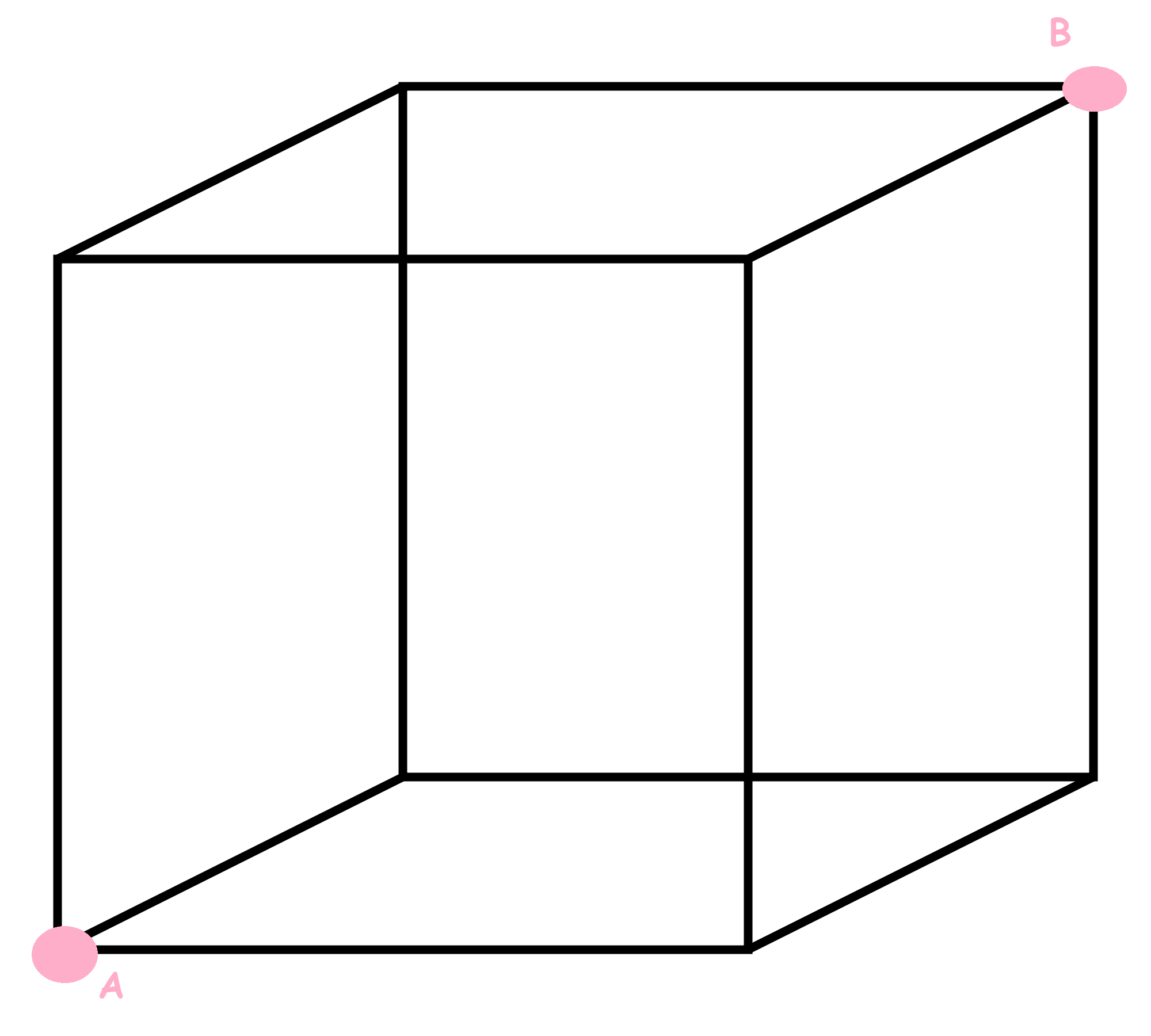
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Oh my.
Yes, I know about 2 d version for resistors and fourier series for getting across square diagonal 2r/pi.[you know that Ishan :D ] But this is quite different fom those, much more difficult in getting the approach. You should share this so that someone reaches at the final ansWeR.
Here is the 2-d version of the problem.
A simpler version would be two find the equivalent resistance between two diagonally opposite points in an infinite grid of resistors, which is still quite difficult. See the page I have linked Infinite grid of resistors
It must be R/3
Log in to reply
Solution ?
I asked for diagonally opposite points. Not adjacent ones
Total resistance (across points A and B) = ( 5/6 ) * R
I can't post a picture of my solution here
Log in to reply
Incorrect, This answer holds if there was a single cube of resistances rather than an infinite one.
Log in to reply
Yes it is haha, I considered only a 'cube'.
but infinite series of resistors just push the "single cube value" to an exact number so my idea is that effective resistance is near (5/6)R (like 0.85R or 0.9R max but not less than (5/6)R). Please notify me if there is a mistake in my assumption.
Log in to reply
I could not understand "push the single cube value to an exact number". Also think of 2-D grid of infinite resistors in which we have to find the equivalent resistance between adjacent points which everyone knows to be R/2. What will be your argument in this one? Just because other resistances are present does not mean that the net would be greater than 5R/6 because resistances in parallel decrease the value
Now what significance pushing values is of, the question is not an mcq, I want to know how it can be done, and I am sure that it is solvable. {although answer would not be beautiful perhaps}.
Log in to reply
got it but I dont know how to solve the way you told and yes the answer sure will be weird
Log in to reply
NO, IT IS NOT SO. In the fourier series , steps of integration are nasty, but answer is simply 2r/ π
Log in to reply
thanks for the info I will surely try to get the steps for your answer.
see 2nd answer to the question in the link https://physics.stackexchange.com/questions/2072/on-this-infinite-grid-of-resistors-whats-the-equivalent-resistance It's for n dimensional grid