Infinite Series that $= \pi$ or $= \pi^2$

Yesterday night, I was looking for an infinite series that equals to $\pi$ . And I found one! Using WolframAlpha's Infinite Series Calculator, I got: 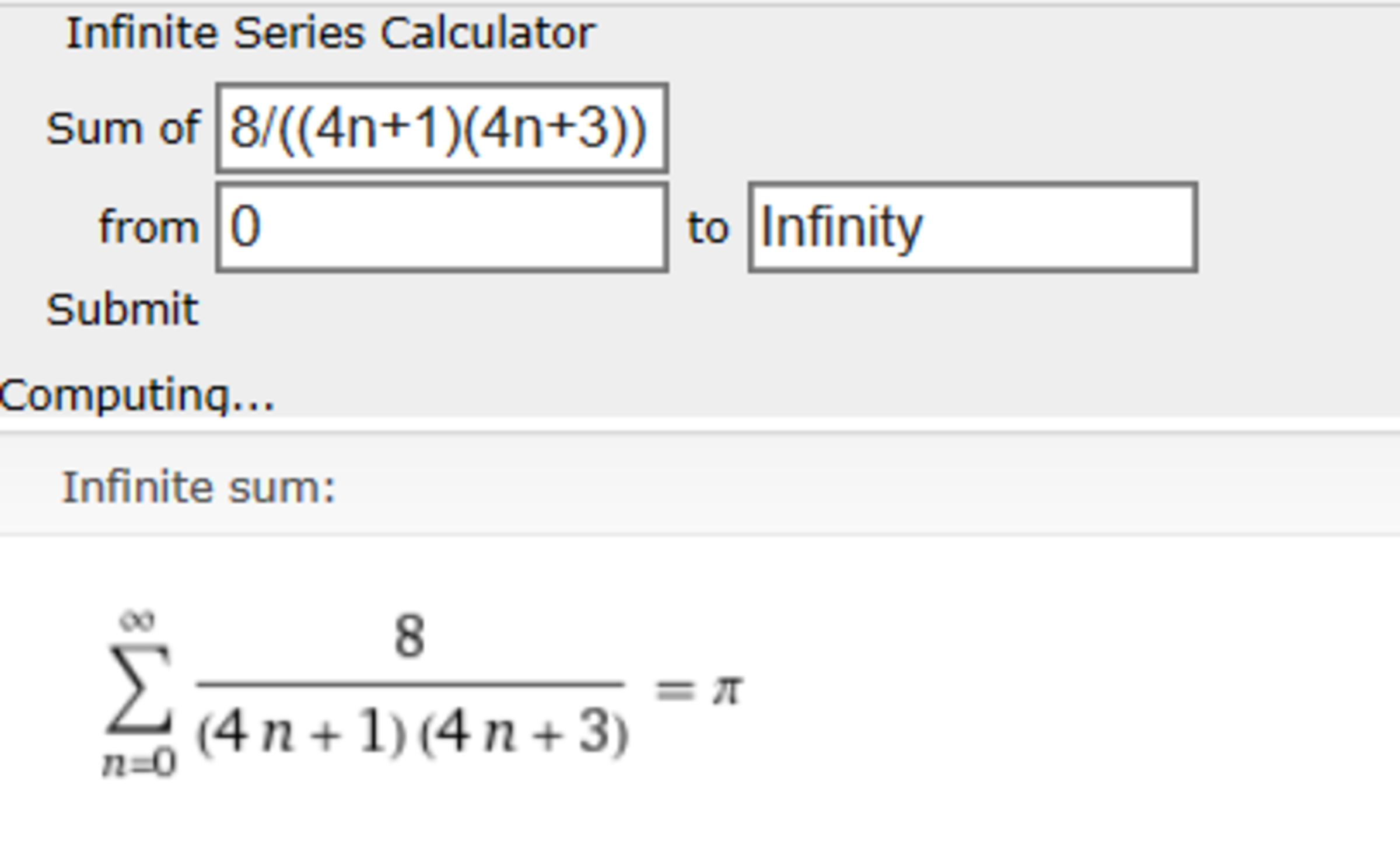It was derived from: $\displaystyle\sum_{n=0}^{\infty} \frac{1}{(4n + 1)(4n + 3)} = \frac{\pi}{8}$

I also found an infinite series that converges to $\pi^2$ :

$\displaystyle\sum_{n=0}^{\infty} \frac{6}{(n + 1)^2} = \pi^2$

It was derived from:

$\displaystyle\sum_{n=0}^{\infty} \frac{1}{(n + 1)^2} = \frac{\pi^2}{6}$

I hope you enjoyed this article and comment if you find any other series that converges to $\pi^2$ or $\pi$ - must be in LaTeX!

Calculus

Algebra

#Calculus

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$\pi$ = $\sum_{n=1}^{\infty}\frac{\Gamma(n-1/2)\Gamma(1/2+1)}{\Gamma(n+1)}$ .Hope you like it.

Aruna Yumlembam - 1 year ago

Ok... @Aruna Yumlembam

A Former Brilliant Member - 1 year ago

The proof relies on the iterated properties of beta function.Check the discussion.

Aruna Yumlembam - 1 year ago

@Aruna Yumlembam – I did - it's great but I am in Year 10, becoming Year 11. How can I do calculus then?

A Former Brilliant Member - 1 year ago

Well I didn't discovered calculus until I was at last year of becoming 10.You know it's never too late to learn something new.

Aruna Yumlembam - 12 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Infinite Series that =π= \pi=π or =π2= \pi^2=π2

Calculus

Algebra

Comments

Infinite Series that $= \pi$ or $= \pi^2$