INMO Practice Board 2015-16
As some of you may know,a Brilliant member,Srihari B,has qualified RMO 2015 and is now preparing himself for INMO 2016,which is to be held on the 17th of January 2016.Although RMO results have only been posted for Mumbai region,others are on their way.This note has been created solely for helping INMO 2016 participants.Let us start posting INMO level problems and help each other prepare,in case we qualify :P.Previous year's INMO participants are kindly requested to help us novices by suggesting books and posting problems.Brilliant members are requested to post relevant and useful comments or doubts.
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Q1) If
n=1∑∞⎝⎛n+100100⎠⎞∑m=1nm1=qp
for some relatively prime positive integers p and q. Find p+q.
Bonus:- Remove 100 and generalise it for some positive integer k.
Q2) Prove that the fraction 14n+321n+4 is irreducible for any natural number n.
Q3)In a concert, 20 singers will perform. For each singer, there is a (possibly empty) set of other singers such that he wishes to perform later than all the singers from that set. Can it happen that there are exactly 2010 orders of the singers such that all their wishes are satisfied?
Q4) A unit square is dissected into n>1 rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square.
Q5) The diagonals of a trapezoid ABCD intersect at point P. Point Q lies between the parallel lines BC and AD such that ∠AQD=∠CQB, and line CD separates points P and Q. Prove that ∠BQP=∠DAQ.
Q6) Let ABCDE be a convex pentagon such that BC∥AE, AB=BC+AE, and ∠ABC=∠CDE. Let M be the midpoint of CE, and let O be the circumcenter of triangle BCD. Given that DMO=90o, prove that 2∠BDA=∠CDE.
Log in to reply
2) 3(14n+3)−2(21n+4)=1 this is bezout lemma so proved.
Log in to reply
According to Bezout Lemma, if ax+by=1 then gcd(a,b) = 1. Now if gcd(a,b)=1 then its obvious that a/b is irreducible.
Log in to reply
Let me show it to you using the basics
14n+321n+4=1+14n+37n+1=1+21[1−14n+31]
Rest depends upon you.
Log in to reply
gcd(21n+4,14n+3)=gcd(14n+3,7n+1)=gcd(7n+1,7n+2)=1. Hence the fraction is irreducible for all natural number n.
I know that's easy but if you edit your post to make it easy for the readers to read.
Q5) Consider a homothety H with centre P that sends A to C ( and hence B to D). Let H send Q to R. Observe that ∠AQD=∠CQB=∠ARD, so A,D,Q,R are concyclic points. Therefore ∠BQP=∠DRP=∠DRQ=∠DAQ.
Log in to reply
Oh nice, just saw it now. I would like to talk to you here's my mail address: [email protected]
Prove that x(x+1)(x+2)(x+3)=y2 has no solution for x,y∈N.
Log in to reply
Maybe I got the solution for this question .... please check though as I am quite bad at proof writing. My solution is as follows:
x(x+1)(x+2)(x+3)={x(x+3)}{(x+1)(x+2)}=(x^2+3.x)(x^2+3.x+2)=y^2. Now note that the gcd(x^2+3x , x^2+3x+2)=2 for all x in N. So x^2+3.x =2.a and x^2+3.x+2=2.b where (a,b)=1. Thus (2.a)(2.b)=y^2. And thus a.b is also a perfect square and (a,b)=1 so we obtain that a=c^2 and b=d^2. where (c,d) is also equal to 1. Thus we have 1+a^2=b^2. So a=0 and b=1 is the only solution but then x will have to be 0 and since x is a natural number this possibility is ruled out. Hence no solution.
Log in to reply
Your solution is perfectly correct! Nicely done!
So here is a geometry problem. A triangle ABC has angle ACB > angle ABC. The internal bisector of angle BAC meets BC at D. The point E on AB is such that angle EDB=90 degrees. The point F on AC such that angle BED=angle DEF. Show that angle BAD=angle FDC
Log in to reply
Ok so does anyone want a solution ? @Shourya Pandey are you solving ?
I have a trigonometry solution that is simple. I'll just post a brief outline.
Show that the problem is equivalent to proving that AD2=AF∗AB.
ADAF=AEADAEAF, and simplify the expression, using sine rule and half-angle formulae, to ABAD.
Log in to reply
Ya that is a nice solution. This is a BMO Level 2 question. I don't know what the official solution is, but i solved this question using pure geometry as follows. Observe that D is the excentre opposite to A for triangle AFE. Hence we obtain that angles DFC and DFE are equal. Extend EF to meet BC at X. Note that triangles BED and XED are congruent. Now do some angle chasing and you are done. :)
Nice one I have a bit simpler proof using pure geometry.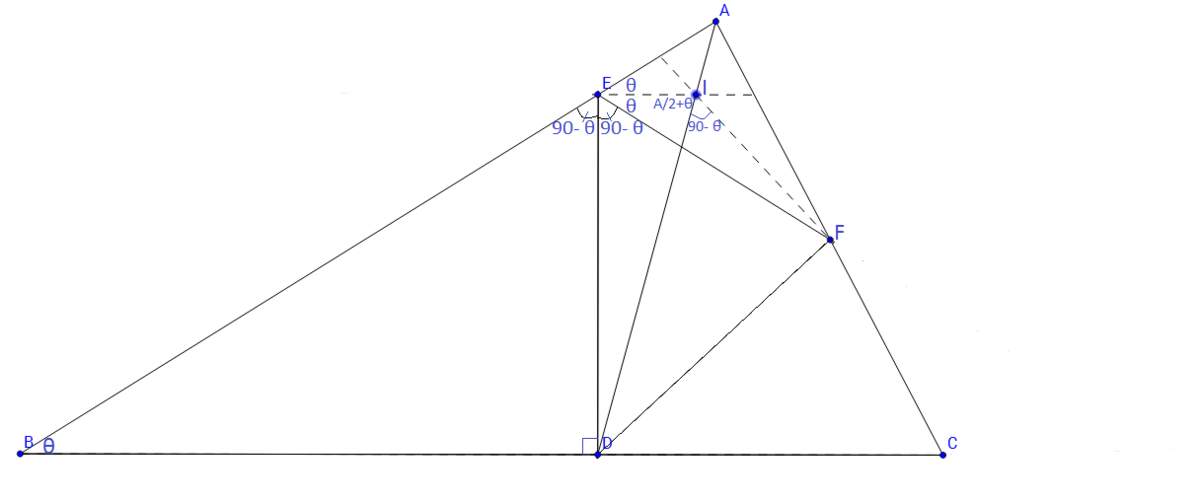
Log in to reply
@Shourya Pandey Let ∠B = θ
The constructions are clearly shown in the above diagram. In △AEF, Draw EI and FI the angle bisectors of ∠AEF and ∠AFE respectively.
∠BED = ∠DEF ---- Given => ∠BED = ∠DEF = 90∘ - θ => ∠AEF = 2θ => ∠AEI = θ
=>∠EID=∠A/2+θ But also, ∠EIF = 90+∠A/2 Therefore: ∠FID=∠EIF−∠EID =90∘ - θ.
So, ∠DEF = ∠FID [= 90−θ ] => Quadrilateral EIFD is a cyclic quad. => ∠FDI = ∠FEI = θ = ∠B. => ∠ADF=∠FDI=θ
Clearly,, ∠ADC=∠ABD+∠BAD
=> ∠ADF+∠FDC=∠ABD+∠BAD
=> θ+∠FDC=θ+∠BAD => ∠FDC=∠BAD
K.I.P.K.I.G.
@Shourya Pandey since you are an IMO bronze medalist can you please suggest how to prepare for INMO ? Basically the problem is that I don't know homothety and complicated stuff like that. I just know basics required at the RMO level. So does that suffice for INMO ? What else other than RMO basics must be known ?
Log in to reply
Just a lot of problem solving will suffice for INMO. But you may keep studying stuff like homothety,etc. , side-by-side . It is really simple, and is only a formal way of writing down your intuition. You can check out the Mathematical Excalibur, which has very good solved and unsolved problems (but don't give in to the solutions before trying; this teaches you a 1000 ways NOT to approach a certain genre of problem).
Log in to reply
Shourya,is it enough if to qualify INMO if have completed these books sufficiently ?:
1) Number Theory-structures, problems , examples by Titu Andreescu 2)Challenges and thrills from the pre-college mathematics-HBCE,TIFR 3)Problem Solving strategies -Arthur engel 4)Concise geometry-MAA 5)101 problems in algebra from MOSP-titu 6)IMO COMPENIUM 7)LAST 15 YEARS INMO PAPERS 8)MATHEMATICAL OLYMPIAD TREASURES-TITU 9)Problem primer for the olympiads-BJ VENKATCHALA
Log in to reply
Wow. You may even make it to the IMO, if you have done ALL of that.
Log in to reply
Ok, then it will be my target and by next year (in class 11th) i will try to complete all these books and then go for RMO.
You can also solve number theory problems from the set "INMO 2016 PRACTICE SET-1" posted by me, if you want. It contains only 6 number theory problems.
If a1,a2,…,an∈Z are distinct, prove that (x−a1)(x−a2)…(x−an)−1 is irreducible.
Log in to reply
Hi ... can u please explain what irreducible means here ? Does it mean that it cannot have even one factor (x-c) ... where c belongs to Z .... or c could be in the R ?
Log in to reply
Yes
Log in to reply
Sorry I didn't get u. That "yes" was for what ? c in Z or c in R ?
Log in to reply
c in Z
Log in to reply
Ok thanks. U have got a really nice set of problems....
Hey I have also attempted this question. Please check my solution.....
Let us assume that the given expression is reducible. So there must be at least one factor say (x-c). Thus we have (c-a1)(c-a2)......(c-an)=1.
CASE A: Let n>2 :- Since the product of n factors is 1 and all the factors are integers, we must have each factor either 1 or -1. Now n>2 and hence by PHP there must be two factors which must be both 1 or both -1. Let those two factors be (c-ai) and (c-aj). Since both are equal hence ai=aj ... a contradiction. Hence there are no solutions for n>2.
CASE B:- n=2. So the two factors are (x-a1) and (x-a2). And their product is 1. So both must be 1 or both must be -1 which yields a1=a2 which again is a contradiction. Hence no solutions for n=2.
Thus we conclude that for all n>1 the expression is irreducible.
Prove that there are infinitely many powers of 2 in the sequence ⌊n2⌋
Log in to reply
Set n=2x2 for some positive integer x.
Log in to reply
I thought about that too but I guess then the question is trivial. I guess he meant that n is natural no.
Log in to reply
Yes maybe.
Hey Svatejas ... can u post solutions of previous questions and post some new questions too ?
Log in to reply
I will be posting the solutions soon. It will be better if you try to solve them yourself. I will also post some more problems soon. Any topic preference you have for problems?
Log in to reply
Yea I will be trying till u post the solutions No priority as such .. but u could give a mixture of NT,Combi,Algebra and Geometry( if u want to and have some qs)
Log in to reply
There are(were) three other RMO boards. Check these links.
https://brilliant.org/discussions/thread/rmo-2015/,
https://brilliant.org/discussions/thread/rmo-board/,
https://brilliant.org/discussions/thread/rmo-board-part-2/.
Prove that y2=x3+7 has no integral solutions.
Hey guys just one day to go for INMO. So i guess its the right time to discuss some basic geometrical lemmas which are strongly used in the tougher problems. So we start posting some lemmas that we know. Its better to go through them before the INMO. So The first lemma: The reflection of the orthocenter on any side of a triangle lies on the circumcircle of the triangle. Please post some useful lemmas like this everyone !!!
Any news about result of RMO of rajasthan region
Log in to reply
You can check it on hbcse site.
Someone please post some good geometry problem. Not from the past RMO or INMO papers please !
Log in to reply
Check these sets
https://brilliant.org/profile/xuming-66nh7b/sets/my-geometry-challenges/
[https://brilliant.org/profile/xuming-66nh7b/sets/my-geometry-proof-challenges/] (https://brilliant.org/profile/xuming-66nh7b/sets/my-geometry-proof-challenges/)
Hint needed ? Or do you guys want to try more ?
@Nihar Mahajan Your geometry is excellent. Could you post some geometry problem ? Not from previous papers
Find the values of n>6 for which n! + 1 is a perfect square. n belongs to Integers
Log in to reply
I believe the answer is no such n exist for n>6
Log in to reply
7!+1=712 . It is the only solution known till date (other than 25=4!+1 and 121=5!+1, but here Rajdeep asked for solutions where n>6).
Log in to reply
Thanks for the solution, but I think I went some where wrong in my solution.
This is the Brocard's problem, and is still open.
Log in to reply
Ok, Thanks
Students selected for INMO 2016 can solve problems from the set "INMO 2016 PRACTICE SET-1" posted by me. It contains 6 number theory problems only. I will be posting other sets for different topics.
Log in to reply
Loved your problem set and i am dying to hear about geometry and algebra problem sets too :)
Log in to reply
Thanks! I will be posting the sets by next 5 days.
This problem is quite similar to one problem of this year's RMO. Prove that there are infinitely many integer solutions to the equation x2+y2+z2=x3+y3+z3.
Log in to reply
Maybe I got this question. But I don't know if such an approach is allowed or no. So please check.My solution is as follows :
We look at (x,y,z) which are in AP. Let x=a-d, y=a ,z=a+d. Now when we substitute these values in the given equation we obtain another equation given by : 3a^2 + 2d^2 = 3a^3+6.a.d^2. Thus d^2 comes out to be 3.a^2.(a-1)/2. Now a^2 is already a perfect square thus 3.(a-1)/2 must be a perfect square. Now note that a=2.3^(2n+1)+1 satisfies the need.From this we can easily find the value of d and hence x,y,z. Already we have a trivial solution (x,y,z)=(1,1,1),(1,0,1).Hence by induction we have infinite solutions for this equation.
Log in to reply
Your solution is correct but there is a much easier may to solve this problem. Such approaches are perfectly allowed. For example, in a RMO question for this years paper, it asked to prove that there are infinitely many integral solutions for the equation x3+y4=z31. One can simply substitute y as 0 and x as n31 and z as n3 where n is an integer. Similar substitutions of setting one variable to 0 also works.
Log in to reply
Ok thanks for that.
Thanks for your contributions to the INMO practise board. I hope u will keep posting such wonderful problems and solutions ...
Log in to reply
Check out the Brilliant Inequality Contest and the Brilliant Polynomial Roots Contest. There have been some inequality and polynomial related questions in INMO so you can expect them too!
Log in to reply
Sure thanks !
a,b∈N are such that ba+1+ab+1∈N. Let d=gcd(a,b). Prove that d2≤a+b
Does there exist a solution for the equation x2+y3=z4 for prime x,y,z?
Log in to reply
Ok I tried this one too.... but please check my solution.....
Let x,y,z all be odd primes. Hence LHS would be even while the RHS would be odd which is absurd. Also note that if two primes are equal then it again leads to a contradiction...check the parity and if all three are 2's then it does not yield a solution..... Hence we conclude that only one of x,y,z is 2.
CASE A: x=2..... Then we have y^3+4=z^4. We know that any prime is either 1 or -1 modulo 6. Thus y^3 is congruent to either 1 or -1 modulo 6. Thus y^3+4 is congruent to either 3 or 5 modulo 6. But note that z^4 is always congruent to 1 modulo 6... which is a contradiction. Hence x=2 is impossible.
CASE B: y=2.... In that case we can factorize the above expression to (z^2+x)(z^2-x)=8. Checking various possibilities we can show that there is no solution for this case too....
CASE C: z=2. Thus we have x^2+y^3=16. x cannot be 2 we have shown that earlier. Thus if x=3 or x=4 then there is no solution and for x>=5 the LHS exceeds the RHS.
Hence there is no solution for any primes x,y,z.
Log in to reply
perfectly correct!
Log in to reply
Thanks ... I am trying the other now ..... U have got a really nice problem collection
Log in to reply
I only have some of the books recommended for the olympiads. How many books do you have?
Log in to reply
I have the following books only ... 1) Challenges and Thrills of Pre-college mathematics 2) An excursion in mathematics 3) I am ordering a book called Inequalities - An approach through problems by B.J.Venkatachala
I mostly never open these books though ... as U may have seen I am almost always online .... that's the best place to study for olympiads
and BTW, Happy New Year!
Log in to reply
Oh yea .... I completely forgot about that .. HAPPY NEW YEAR !!!
Find all polynomials p such that p(x+1)=p(x)+2x+1.
Log in to reply
Is x any real number in this question ?
You first choose any two positive integers a,b and replace them with gcd(a,b) and lcm(a,b). Prove that eventually, the numbers will stop changing.
Log in to reply
Hey in this question once we replace a,b by lcm(a,b) and gcd(a,b) then won't they be constant after that forever ? Because gcd(gcd(a,b),lcm(a,b))=gcd(a,b) and lcm(gcd(a,b),lcm(a,b))=lcm(a,b). Or am i misinterpreting the question ?
Log in to reply
Yes you have. I guess the problem hasn't been framed properly. You replace one with gcd and the other with lcm.
Log in to reply
Sorry for disturbing but could u add an example for the above question ? Taking some random but nice example ? I haven't understood it properly....
Log in to reply
Take a as 20 and b as 16. gcd(20,16)=4 and lcm(20,16)=80. gcd(4,80)=4 and lcm(4,80)=80. This continues.
@Shourya Pandey I want a demonstration of how to solve this question using homothety..can u pls help me with a solution ? Question is as follows :
X and Y are two circles touching internally at T(X is inside Y). A chord AB of Y is tangent to X at P. Line TP meets Y again at Q. Prove that Q is the midpoint of arc AQB of Y.
Prove that if a positive integer can be expressed as a sum of three squares, then its square can also be expressed as a sum of three squares. In other words, prove that if n=a2+b2+c2, then n2=x2+y2+z2 where n,a,b,c,x,y,z∈N.
If n≥3, then prove that 2n can be represented in the form 7x2+y2 where x and y are odd. (very hard)
Log in to reply
Both these ques are ditto from problem solving strategies by arthur Engel
If q=ab+1a2+b2 where a,b,q∈Z, prove that q is a perfect square. (very hard)
Log in to reply
Counterexample : a=4,b=3.
Log in to reply
q must be an integer
Log in to reply
Then please edit the question.
Log in to reply
Sorry I put Q for Z
This problem must be read as this expression is a perfect square if it is an integer
Prove that the equation x2+y2+z2=2xyz has no integral solution except x=y=z=0.
Extension Prove that the equation x2+y2+z2=kxyz has infinitely many solutions only for k=1 and k=3.
Log in to reply
A simple use of fermat s infinite descent
Same problem is in MATHEMATICAL OLYMPIAD CHALLENGES by TITU ANDREESCU.
If n∈N and 4n+2n+1 is prime, prove that n is a power of 3.
Log in to reply
try the new question for proof contest (https://brilliant.org/profile/lakshya-a71u6y/sets/proof-contest/)
Log in to reply
Thanks. I will take a look at it.
Question:Consider two circles S and R.Let the center of circle S lie on R.Let S and R intersect at A and B.Let C be a point on S such that AB=AC.Then prove that the point of intersection of AC and R lies in or on S.
Log in to reply
It seems that u ve done a typographical error the ans seems trivial
Log in to reply
there is no error