Inspired by Vatsalya Tandon

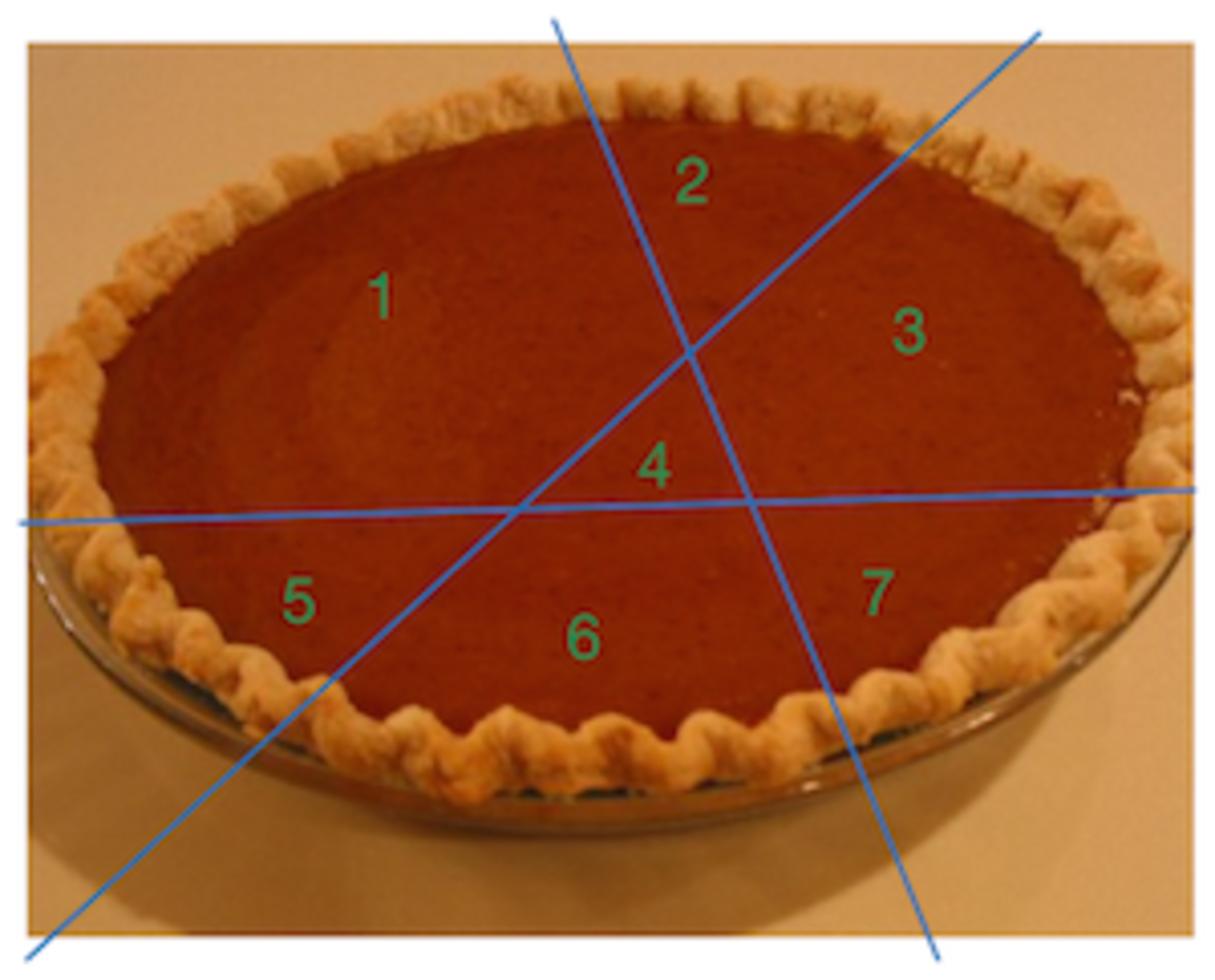
We all know that to cut a (circular) pie,

1 cut gives us at most 2 pieces,
2 cuts give us at most 4 pieces,
3 cuts give us at most 7 pieces.

It is clear for 1 cut and 2 cuts, how we can get these pieces to be the same size.

Can we cut a circular pie into 7 equal pieces with 3 cuts?

If no, why not?

If yes, can we cut a circular pie into 11 equal pieces with 4 cuts?

This thought occurred to me as I was adding an image to Vatsalya's Problem.

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I suspect the answer is no, to either scenario.

In the $3$ cut case, each chord would have to, independently, divide the circle into regions with a $3:4$ area ratio. The chords would also have to be drawn so that an interior triangle is formed. The maximum area of this triangle given these conditions would, by symmetry, be less than one-seventh the area of the circle, (it comes out to roughly one-fifteenth).

In the $4$ cut case, @Michael Mendrin proved for me here that a circle cannot be cut into $9$ regions of equal area using $4$ cuts, so I would assume that $10$ or $11$ regions of equal area are out of the question. (Using circular cuts we can achieve $9$ regions of equal area, as shown here.)

Perhaps we could make the conjecture that the maximum number of regions of equal area that can be created using $n$ cuts is $2n$ .

Brian Charlesworth - 6 years, 6 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$